Start Learning Free
Previous Tutorial
22
DecAbstract Data Type in Data Structures With Example
25 Jul 2024
Beginner
12.8K Views
55 min read
Learn with an interactive course and practical hands-on labs
Free DSA Course with Certificate
Abstract Data Type
Data types specify the type of data structure. We can classify the data type into primitive data types like integer, float, double, etc., or abstract data types like list, stack, queue, etc. Abstract data type (ADT) is a concept or model of a data type. It does not specify how data will be organized in memory and what algorithms will be used for implementing the operations. It is called “abstract” because it gives an implementation-independent view.
In this DSA tutorial, we will discuss Abstract Data Types (ADT). For an in-depth understanding of data structures, consider our DSA Programming Course.
What is an Abstract Data Type?
An Abstract Data Type in data structures is a data type whose behavior is defined with the help of some attributes and some functions. Generally, we write these attributes and functions inside a class or a structure to use an object of the class to use that particular abstract data type. In other words, an ADT provides only the interface to which the data structure must adhere. The interface does not give specific details about what should be implemented or in what programming language.
In every programming language, ADTs are implemented using different methods and logic. We have learned in C that ADTs are implemented mostly using structure. Whereas in C++ or JAVA, they’re implemented using class. However, operations are common in all languages.
Read More:
Abstract Data Type Model
In the above figure, we can see the ADT model. There are two types of models in the ADT model:
- the public function
- the private function
The ADT model also contains the data structures being used in a program. Here, at first, encapsulation is performed, i.e., all the data is wrapped in a single unit, i.e., ADT. Afterwards, abstraction is performed i.e. showing the operations that can be performed on the data structure and also showcasing the data structures being used in a program.
Read More:
Types of Abstract Data Types (ADTs)
There are mainly three types of ADTs:
1. List ADT
Lists are linear data structures stored in a non-continuous manner. The list is made up of a series of connected nodes that are randomly stored in the memory. Here, each node consists of two parts, the first part is the data and the second part contains the pointer to the address of the next node.
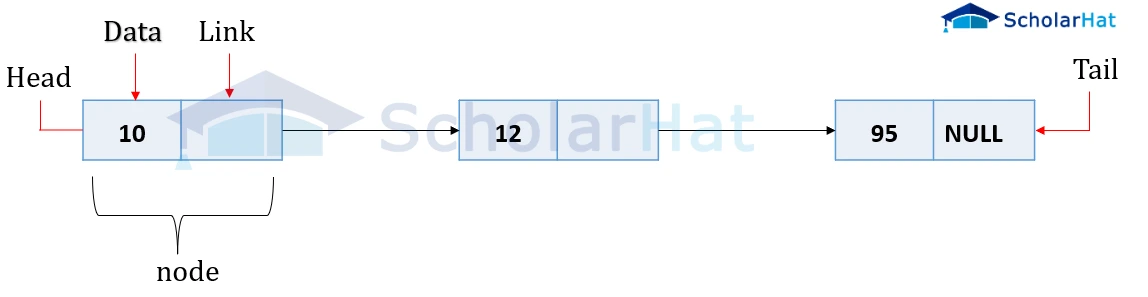
The first node of a linked list is called the Head, and it acts as an access point. The head pointer points to the first element of the linked list. The last node is called the Tail, and it marks the end of a linked list by pointing to a NULL value.
Read More: Linked Lists in Data Structures
The List ADT functions/operations are as follows:
- front(): returns the value of the node present at the front of the list.
- back(): returns the value of the node present at the back of the list.
- push_front(int val): creates a pointer with value = val and keeps this pointer to the front of the linked list.
- push_back(int val): creates a pointer with value = val and keeps this pointer to the back of the linked list.
- pop_front(): removes the front node from the list.
- pop_back(): removes the last node from the list.
- empty(): returns true if the list is empty, otherwise returns false.
- size(): returns the number of nodes present in the list.
Example illustrating List ADT Operations
class Node:
def __init__(self, val):
self.data = val # to store the data
self.next = None # to store the address of the next List node
class List:
def __init__(self):
self.head = None # pointer to the head of the linked list
self.count = 0 # to count the number of nodes in the list
def front(self): # returns value of the node present at the front of the list
if self.head:
return self.head.data
else:
raise Exception("List is empty")
def back(self): # returns value of the node present at the back of the list
if self.head:
temp = self.head
while temp.next:
temp = temp.next
return temp.data
else:
raise Exception("List is empty")
def push_front(self, val): # creates a pointer with value = val and keeps this pointer to the front of the linked list
newNode = Node(val)
newNode.next = self.head
self.head = newNode
self.count += 1
def push_back(self, val): # creates a pointer with value = val and keeps this pointer to the back of the linked list
newNode = Node(val)
if not self.head:
self.head = newNode
else:
temp = self.head
while temp.next:
temp = temp.next
temp.next = newNode
self.count += 1
def pop_front(self): # removes the front node from the list
if self.head:
temp = self.head
self.head = self.head.next
temp.next = None
self.count -= 1
else:
raise Exception("List is empty")
def pop_back(self): # removes the last node from the list
if self.head:
if not self.head.next:
self.head = None
else:
temp = self.head
while temp.next.next:
temp = temp.next
temp.next = None
self.count -= 1
else:
raise Exception("List is empty")
def empty(self): # returns true if list is empty, otherwise returns false
return self.count == 0
def size(self): # returns the number of nodes that are present in the list
return self.count
# Test the List class
myList = List()
# Test operations
myList.push_back(1)
myList.push_back(2)
myList.push_back(3)
print("Front of the list:", myList.front())
print("Back of the list:", myList.back())
print("List size:", myList.size())
myList.pop_front()
myList.pop_back()
print("Front of the list after pop_front():", myList.front())
print("Back of the list after pop_back():", myList.back())
import java.util.NoSuchElementException;
// Defining node of the list
class Node {
int data; // to store the data
Node next; // to store the address of the next List node
// Constructor to initialize the node parameters
Node(int val) {
data = val;
next = null;
}
}
class List {
int count = 0; // to count the number of nodes in the list
Node head; // pointer to the head of the linked list
// Constructor
List() {
head = null;
}
int front() { // returns value of the node present at the front of the list
if (head != null)
return head.data;
else
throw new NoSuchElementException("List is empty");
}
int back() { // returns value of the node present at the back of the list
if (head != null) {
Node temp = head;
while (temp.next != null)
temp = temp.next;
return temp.data;
} else
throw new NoSuchElementException("List is empty");
}
void push_front(int val) { // creates a pointer with value = val and keeps this pointer to the front of the linked list
Node newNode = new Node(val);
newNode.next = head;
head = newNode;
count++;
}
void push_back(int val) { // creates a pointer with value = val and keeps this pointer to the back of the linked list
Node newNode = new Node(val);
if (head == null)
head = newNode;
else {
Node temp = head;
while (temp.next != null)
temp = temp.next;
temp.next = newNode;
}
count++;
}
void pop_front() { // removes the front node from the list
if (head != null) {
Node temp = head;
head = head.next;
temp.next = null;
count--;
} else
throw new NoSuchElementException("List is empty");
}
void pop_back() { // removes the last node from the list
if (head != null) {
if (head.next == null) {
head = null;
} else {
Node temp = head;
while (temp.next.next != null)
temp = temp.next;
temp.next = null;
}
count--;
} else
throw new NoSuchElementException("List is empty");
}
boolean empty() { // returns true if list is empty, otherwise returns false
return count == 0;
}
int size() { // returns the number of nodes that are present in the list
return count;
}
}
public class Main {
public static void main(String[] args) {
List myList = new List();
// Test operations
myList.push_back(1);
myList.push_back(2);
myList.push_back(3);
System.out.println("Front of the list: " + myList.front());
System.out.println("Back of the list: " + myList.back());
System.out.println("List size: " + myList.size());
myList.pop_front();
myList.pop_back();
System.out.println("Front of the list after pop_front(): " + myList.front());
System.out.println("Back of the list after pop_back(): " + myList.back());
}
}
#include <iostream>
using namespace std;
// Defining node of the list
class Node {
public:
int data; // to store the data
Node* next; // to store the address of the next List node
// Constructor to initialize the node parameters
Node(int val) {
data = val;
next = NULL;
}
};
class List {
int count = 0; // to count the number of nodes in the list
Node* head; // pointer to the head of the linked list
public:
// Constructor
List() {
head = NULL;
}
// Destructor
~List() {
while (head != NULL) {
Node* temp = head;
head = head->next;
delete temp;
}
}
int front(); // returns value of the node present at the front of the list
int back(); // returns value of the node present at the back of the list
void push_front(int val); // creates a pointer with value = val and keeps this pointer to the front of the linked list
void push_back(int val); // creates a pointer with value = val and keeps this pointer to the back of the linked list
void pop_front(); // removes the front node from the list
void pop_back(); // removes the last node from the list
bool empty(); // returns true if list is empty, otherwise returns false
int size(); // returns the number of nodes that are present in the list
};
int List::front() {
if (head != NULL)
return head->data;
else
throw out_of_range("List is empty");
}
int List::back() {
if (head != NULL) {
Node* temp = head;
while (temp->next != NULL)
temp = temp->next;
return temp->data;
}
else
throw out_of_range("List is empty");
}
void List::push_front(int val) {
Node* newNode = new Node(val);
newNode->next = head;
head = newNode;
count++;
}
void List::push_back(int val) {
Node* newNode = new Node(val);
if (head == NULL)
head = newNode;
else {
Node* temp = head;
while (temp->next != NULL)
temp = temp->next;
temp->next = newNode;
}
count++;
}
void List::pop_front() {
if (head != NULL) {
Node* temp = head;
head = head->next;
delete temp;
count--;
}
else
throw out_of_range("List is empty");
}
void List::pop_back() {
if (head != NULL) {
if (head->next == NULL) {
delete head;
head = NULL;
}
else {
Node* temp = head;
while (temp->next->next != NULL)
temp = temp->next;
delete temp->next;
temp->next = NULL;
}
count--;
}
else
throw out_of_range("List is empty");
}
bool List::empty() {
return count == 0;
}
int List::size() {
return count;
}
int main() {
List myList;
// Test operations
myList.push_back(1);
myList.push_back(2);
myList.push_back(3);
cout << "Front of the list: " << myList.front() << endl;
cout << "Back of the list: " << myList.back() << endl;
cout << "List size: " << myList.size() << endl;
myList.pop_front();
myList.pop_back();
cout << "Front of the list after pop_front(): " << myList.front() << endl;
cout << "Back of the list after pop_back(): " << myList.back() << endl;
return 0;
}
The above program demonstrates the working of the LIST ADT functions in three different programming languages.
Output
Front of the list: 1
Back of the list: 3
List size: 3
Front of the list after pop_front(): 2
Back of the list after pop_back(): 2 2. Queue ADT
A queue is an ordered list in which insertion is done at one end called REAR and deletion at another end called FRONT. The first inserted element is available first for the operations to be performed and is the first one to be deleted. Hence, it is known as First In First Out, FIFO, or Last In Last Out, LILO.
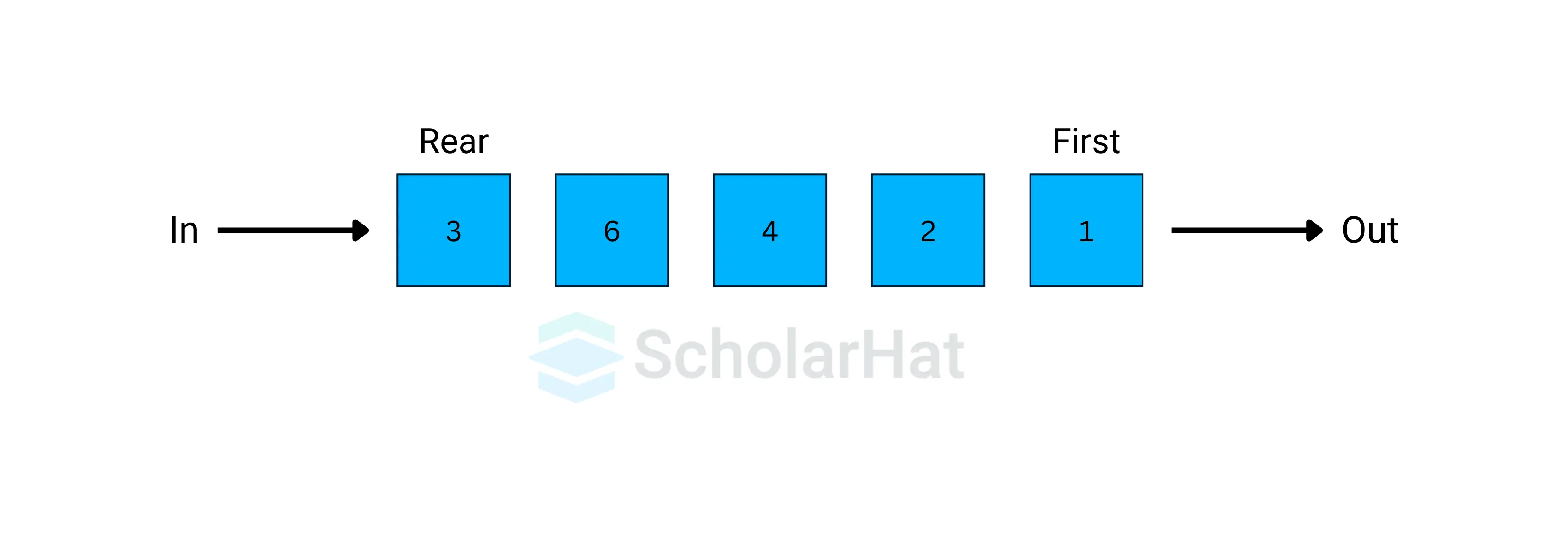
Read More: Queue in Data Structures
The Queue ADT functions/operations are as follows:
- enqueue(): Insert an element at the end of the queue.
- dequeue(): Remove and return the first element of the queue, if the queue isn't empty.
- peek(): Return the element from the queue without removing it.
- size(): Return the number of elements in the queue.
- isEmpty(): Return true if the queue is empty, otherwise return false.
- isFull(): Return true if the queue is full, otherwise return false.
Example Illustrating Queue ADT Operations
class Node:
def __init__(self, val):
self.data = val # to store data in a stack node
self.next = None # to store the address of the next node in the stack
class Queue:
def __init__(self):
self.count = 0 # to count number of nodes in the stack
self.frontNode = None # pointer to the front of the queue
self.rearNode = None # pointer to the rear of the queue
# Returns value of the node present at the front of the queue
def front(self):
if self.frontNode is not None:
return self.frontNode.data
else:
raise IndexError("Queue is empty")
# Returns value of the node present at the back of the queue
def back(self):
if self.rearNode is not None:
return self.rearNode.data
else:
raise IndexError("Queue is empty")
# Creates a node with value = val and put it at the front of the queue
def push(self, val):
newNode = Node(val)
if self.frontNode is None:
self.frontNode = newNode
self.rearNode = newNode
else:
self.rearNode.next = newNode
self.rearNode = newNode
self.count += 1
# Removes node from the front of the queue
def pop(self):
if self.frontNode is not None:
self.frontNode = self.frontNode.next
self.count -= 1
if self.frontNode is None:
self.rearNode = None
else:
raise IndexError("Queue is empty")
# Returns true if queue is empty, otherwise returns false
def empty(self):
return self.count == 0
# Returns the number of nodes that are present in the queue
def size(self):
return self.count
# Test the Queue class
myQueue = Queue()
# Test operations
myQueue.push(1)
myQueue.push(2)
myQueue.push(3)
print("Front of the queue:", myQueue.front())
print("Back of the queue:", myQueue.back())
print("Queue size:", myQueue.size())
myQueue.pop()
print("Front of the queue after pop():", myQueue.front())
class Node {
public int data; // to store data in a stack node
public Node next; // to store the address of the next node in the stack
// Constructor to initialize stack parameters
public Node(int val) {
data = val;
next = null;
}
}
class Queue {
private int count = 0; // to count number of nodes in the stack
private Node frontNode; // pointer to the front of the queue
private Node rearNode; // pointer to the rear of the queue
// Returns value of the node present at the front of the queue
public int front() {
if (frontNode != null) {
return frontNode.data;
} else {
throw new IndexOutOfBoundsException("Queue is empty");
}
}
// Returns value of the node present at the back of the queue
public int back() {
if (rearNode != null) {
return rearNode.data;
} else {
throw new IndexOutOfBoundsException("Queue is empty");
}
}
// Creates a node with value = val and put it at the front of the queue
public void push(int val) {
Node newNode = new Node(val);
if (frontNode == null) {
frontNode = newNode;
rearNode = newNode;
} else {
rearNode.next = newNode;
rearNode = newNode;
}
count++;
}
// Removes node from the front of the queue
public void pop() {
if (frontNode != null) {
frontNode = frontNode.next;
count--;
if (frontNode == null) {
rearNode = null;
}
} else {
throw new IndexOutOfBoundsException("Queue is empty");
}
}
// Returns true if queue is empty, otherwise returns false
public boolean empty() {
return count == 0;
}
// Returns the number of nodes that are present in the queue
public int size() {
return count;
}
}
// Test the Queue class
public class Main {
public static void main(String[] args) {
Queue myQueue = new Queue();
// Test operations
myQueue.push(1);
myQueue.push(2);
myQueue.push(3);
System.out.println("Front of the queue: " + myQueue.front());
System.out.println("Back of the queue: " + myQueue.back());
System.out.println("Queue size: " + myQueue.size());
myQueue.pop();
System.out.println("Front of the queue after pop(): " + myQueue.front());
}
}
#include
using namespace std;
class Node {
public:
int data; // to store data in a stack node
Node* next; // to store the address of the next node in the stack
// Constructor to initialize stack parameters
Node(int val) {
data = val;
next = NULL;
}
};
class Queue {
private:
int count = 0; // to count number of nodes in the stack
Node* frontNode; // pointer to the front of the queue
Node* rearNode; // pointer to the rear of the queue
public:
// Constructor
Queue() {
frontNode = NULL;
rearNode = NULL;
}
// Destructor
~Queue() {
while (frontNode != NULL) {
Node* temp = frontNode;
frontNode = frontNode->next;
delete temp;
}
}
// Returns value of the node present at the front of the queue
int front() {
if (frontNode != NULL) {
return frontNode->data;
} else {
throw out_of_range("Queue is empty");
}
}
// Returns value of the node present at the back of the queue
int back() {
if (rearNode != NULL) {
return rearNode->data;
} else {
throw out_of_range("Queue is empty");
}
}
// Creates a node with value = val and put it at the front of the queue
void push(int val) {
Node* newNode = new Node(val);
if (frontNode == NULL) {
frontNode = newNode;
rearNode = newNode;
} else {
rearNode->next = newNode;
rearNode = newNode;
}
count++;
}
// Removes node from the front of the queue
void pop() {
if (frontNode != NULL) {
Node* temp = frontNode;
frontNode = frontNode->next;
delete temp;
count--;
if (frontNode == NULL) {
rearNode = NULL;
}
} else {
throw out_of_range("Queue is empty");
}
}
// Returns true if queue is empty, otherwise returns false
bool empty() {
return count == 0;
}
// Returns the number of nodes that are present in the queue
int size() {
return count;
}
};
// Test the Queue class
int main() {
Queue myQueue;
// Test operations
myQueue.push(1);
myQueue.push(2);
myQueue.push(3);
cout << "Front of the queue: " << myQueue.front() << endl;
cout << "Back of the queue: " << myQueue.back() << endl;
cout << "Queue size: " << myQueue.size() << endl;
myQueue.pop();
cout << "Front of the queue after pop(): " << myQueue.front() << endl;
return 0;
}
The above program demonstrates the working of the Queue ADT functions in three different programming languages.
Output
Front of the queue: 1
Back of the queue: 3
Queue size: 3
Front of the queue after pop(): 2 3. Stack ADT
A stack is an ordered list or we can say a container in which insertion and deletion can be done from the one end known as the top of the stack. The last inserted element is available first and is the first one to be deleted. Hence, it is known as Last In, First Out LIFO, or First In, Last Out FILO.
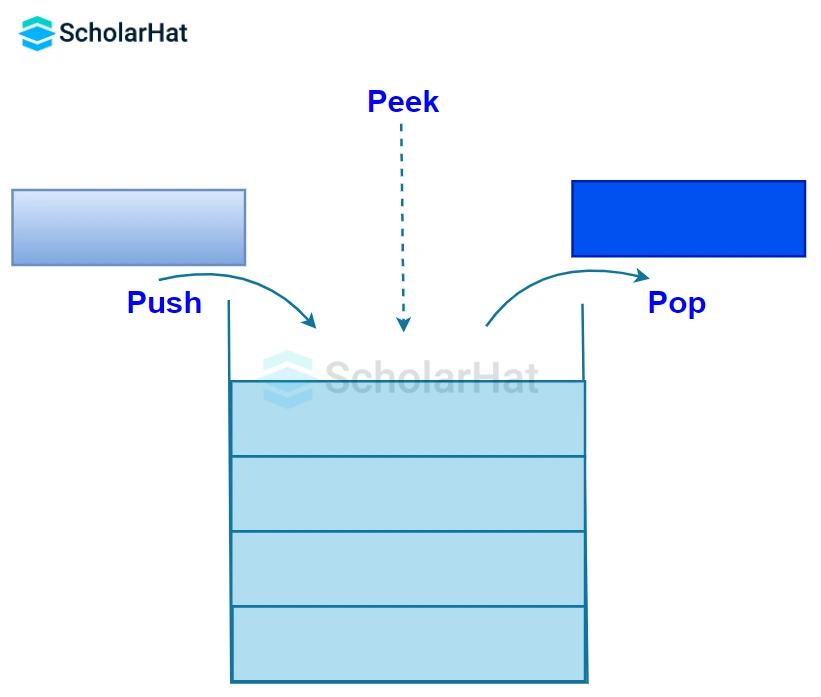
In a stack, the element at the top is known as the top element. When a new element is added to the stack, it is placed on top of the existing elements. Stacks are dynamic; this means that they do not have a fixed size and their size can be increased or decreased depending upon the number of elements.
Read More: Stack in Data Structures
The Stack ADT functions/operations are as follows:
- top(): returns the value of the node present at the top of the stack.
- push(int val): creates a node with value = val and puts it at the stack top.
- pop(): removes the node from the top of the stack.
- empty(): returns true if the stack is empty else false.
- size(): returns the number of nodes present in the stack
Example Illustrating Stack ADT Operations
class Node:
def __init__(self, val):
self.data = val # to store data in a stack node
self.next = None # to store the address of the next node in the stack
class Stack:
def __init__(self):
self.count = 0 # to count number of nodes in the stack
self.topNode = None # pointer to the top of the stack
def top(self): # returns value of the node present at the top of the stack
if self.topNode is not None:
return self.topNode.data
else:
raise IndexError("Stack is empty")
def push(self, val): # creates a node with value = val and put it at the stack top
newNode = Node(val)
newNode.next = self.topNode
self.topNode = newNode
self.count += 1
def pop(self): # removes node from the top of the stack
if self.topNode is not None:
temp = self.topNode
self.topNode = self.topNode.next
temp.next = None
self.count -= 1
else:
raise IndexError("Stack is empty")
def empty(self): # returns true if stack is empty, otherwise returns false
return self.count == 0
def size(self): # returns the number of nodes that are present in the stack
return self.count
# Test the Stack class
myStack = Stack()
# Test operations
myStack.push(1)
myStack.push(2)
myStack.push(3)
print("Top of the stack:", myStack.top())
print("Stack size:", myStack.size())
myStack.pop()
print("Top of the stack after pop():", myStack.top())
import java.util.EmptyStackException;
class Node {
int data; // to store data in a stack node
Node next; // to store the address of the next node in the stack
Node(int val) { // constructor to initialize stack parameters
data = val;
next = null;
}
}
class Stack {
int count = 0; // to count number of nodes in the stack
Node topNode; // pointer to the top of the stack
int top() { // returns value of the node present at the top of the stack
if (topNode != null)
return topNode.data;
else
throw new EmptyStackException();
}
void push(int val) { // creates a node with value = val and put it at the stack top
Node newNode = new Node(val);
newNode.next = topNode;
topNode = newNode;
count++;
}
void pop() { // removes node from the top of the stack
if (topNode != null) {
topNode = topNode.next;
count--;
} else
throw new EmptyStackException();
}
boolean empty() { // returns true if stack is empty, otherwise returns false
return count == 0;
}
int size() { // returns the number of nodes that are present in the stack
return count;
}
}
public class Main {
public static void main(String[] args) {
Stack myStack = new Stack();
// Test operations
myStack.push(1);
myStack.push(2);
myStack.push(3);
System.out.println("Top of the stack: " + myStack.top());
System.out.println("Stack size: " + myStack.size());
myStack.pop();
System.out.println("Top of the stack after pop(): " + myStack.top());
}
}
#include <iostream>
using namespace std;
class Node {
public:
int data; // to store data in a stack node
Node* next; // to store the address of the next node in the stack
Node(int val) { // constructor to initialize stack parameters
data = val;
next = nullptr;
}
};
class Stack {
int count = 0; // to count number of nodes in the stack
Node* topNode; // pointer to the top of the stack
public:
int top() { // returns value of the node present at the top of the stack
if (topNode != nullptr)
return topNode->data;
else
throw out_of_range("Stack is empty");
}
void push(int val) { // creates a node with value = val and put it at the stack top
Node* newNode = new Node(val);
newNode->next = topNode;
topNode = newNode;
count++;
}
void pop() { // removes node from the top of the stack
if (topNode != nullptr) {
Node* temp = topNode;
topNode = topNode->next;
delete temp;
count--;
} else
throw out_of_range("Stack is empty");
}
bool empty() { // returns true if stack is empty, otherwise returns false
return count == 0;
}
int size() { // returns the number of nodes that are present in the stack
return count;
}
};
int main() {
Stack myStack;
// Test operations
myStack.push(1);
myStack.push(2);
myStack.push(3);
cout << "Top of the stack: " << myStack.top() << endl;
cout << "Stack size: " << myStack.size() << endl;
myStack.pop();
cout << "Top of the stack after pop(): " << myStack.top() << endl;
return 0;
}
The above program demonstrates the working of the Stack ADT functions in three different programming languages.
Output
Top of the stack: 3
Stack size: 3
Top of the stack after pop(): 2
Advantages of ADT
- Encapsulation: ADTs help encapsulate data and operations into a single unit, making managing and modifying the data structure easier.
- Abstraction: You can work with ADTs without knowing the implementation details, which can simplify programming and reduce errors.
- Data Structure Independence: ADTs can be implemented using different data structures, to make it easier to adapt to changing needs and requirements.
- Information Hiding: ADTs protect data integrity by controlling access and preventing unauthorized modifications.
- Modularity: ADTs can be combined with other ADTs to form more complex data structures increasing flexibility and modularity in programming.
Disadvantages of ADT
- Overhead: Implementing ADTs can lead to overhead in terms of memory and processing resulting in reduced performance.
- Complexity: ADTs can be complex to implement, especially for large and complex data structures.
- Learning Curve: To learn to implement ADTs takes a good amount of time and effort.
- Limited Flexibility: Some ADTs may be limited in their functionality or may not be suitable for all types of data structures.
- Cost: Implementing ADTs may require additional resources and investment increasing the cost of development.
Applications and Use Cases of ADT
- Data Structures: ADTs are used to implement fundamental data structures like arrays, linked lists, stacks, queues, trees, graphs, hash tables, and heaps.
- Database Management Systems (DBMS): Concepts like tables, rows, columns, and relationships can be represented using ADTs.
- Operating Systems: ADTs are employed in the design and implementation of operating system components such as file systems, process management, memory management, and synchronization mechanisms.
- Compiler Design: ADTs represent and manipulate various components of a compiler like abstract syntax trees, symbol tables, and intermediate code representations.
- Networking: ADTs like queues and buffers are used for storing and managing packets in network switches and routers.
Summary
In this tutorial, we saw in-depth about Abstract Data Types (ADT). We have tried to make you understand through examples of the main ADTs. To understand the whole topic, start with the first data structure tutorial and follow the sequence. If you want to master the concepts of data structures, refer to our Data Structures Certification Course.
FAQs
An abstract data model in data structures defines operations and properties of data independently of implementation, providing a high-level view of data organization and manipulation without specifying internal details.
A stack is called an abstract data type (ADT) because it defines a set of operations (such as push and pop) and properties (such as Last-In-First-Out behavior) without specifying the implementation details.
A struct is considered an abstract data type (ADT) because it encapsulates related data fields and allows us to access and manipulation without exposing the internal implementation details.
Abstract data types (ADTs) are important because they provide a clear and standardized way to conceptualize and interact with data structures, allowing developers to focus on functionality without worrying about implementation details.