19
DecAVL Tree in Data Structures with Examples
AVL Tree in Data Structures: An Overview
We know that the Binary Search Tree cannot guarantee logarithmic complexity. If the elements are inserted in a sorted increasing order, the tree becomes skewed, so the worst-case time complexity for insert/search operations becomesO(n). To overcome this limitation of binary search trees, AVL Trees came into existence.In this DSA tutorial, we will discuss AVL trees, balance factors, rotations of AVL trees, operations, etc. Build a strong foundation for high-paying tech roles with DSA expertise. Enroll in our Free DSA Course today!
What is an AVL Tree in Data Structures?
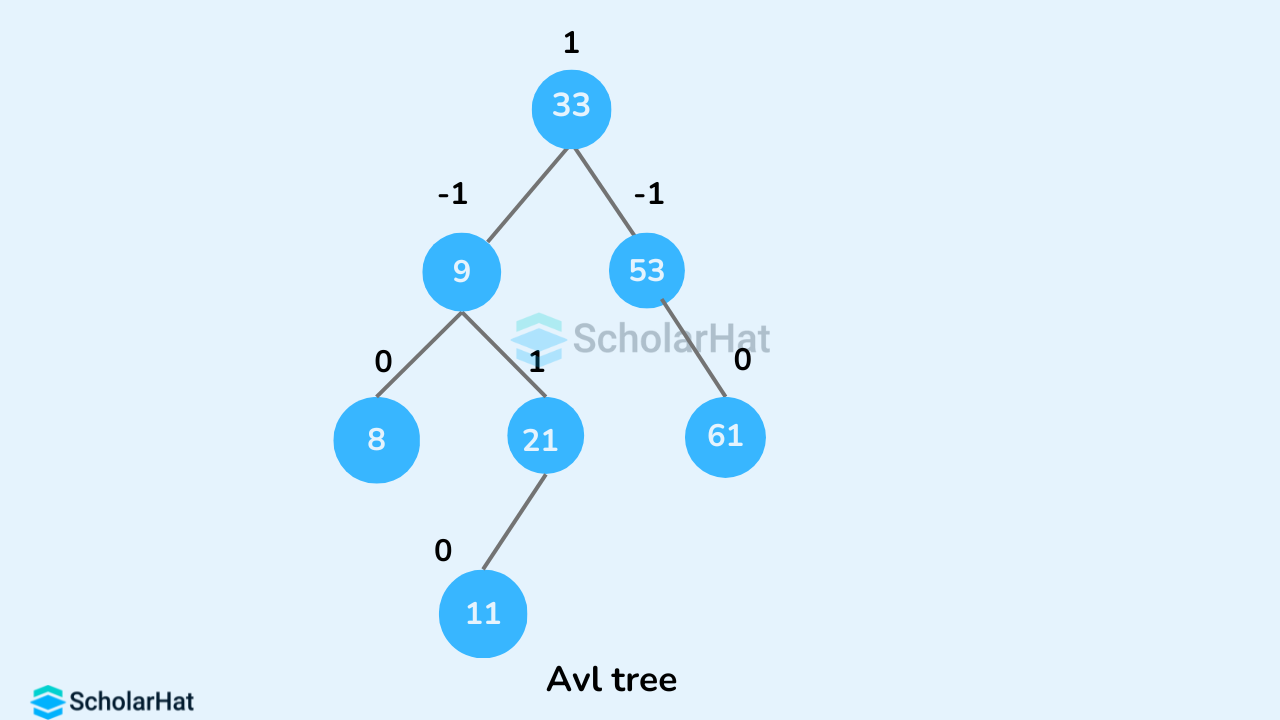
AVL tree in data structures is a popular self-balancing binary search tree where the difference between the heights of left and right subtrees for any node does not exceed unity. It was introduced by Georgy Adelson-Velsky and Evgenii Landis in 1962, hence the name AVL. It automatically adjusts its structure to maintain the minimum possible height after any operation with the help of a balance factor for each node.Balance Factor in AVL Tree in Data Structures
The balance factor of a node in an AVL Tree is a numerical value that represents the difference in height between the left and right subtrees of that node. It is the extra information used to determine the tree's balance. The balance factor is calculated as follows:Balance Factor = height(left subtree) - height(right subtree)
or
bf = hl − hr,
where bf = balance factor of a given node, hl = height of the left subtree, and hr = height of the right subtree.
∣bf∣ = ∣hl − hr∣ ≤ 1
- If the balance factor of any node = 1, the left sub-tree is one level higher than the right sub-tree i.e. the given node is left-heavy.
- If the balance factor of any node = 0, the left sub-tree and right sub-tree are of equal height.
- If the balance factor of any node = -1, the left sub-tree is one level lower than the right sub-tree i.e. the given node is right-heavy.
For leaf nodes, the balance factor is 0 as they do not contain any subtrees.
Hence, in this way, the self-balancing property of an AVL tree is maintained by the balance factor. Thus, we can find an unbalanced node in the tree and locate where the height-affecting operation was performed that caused the imbalance of the tree.
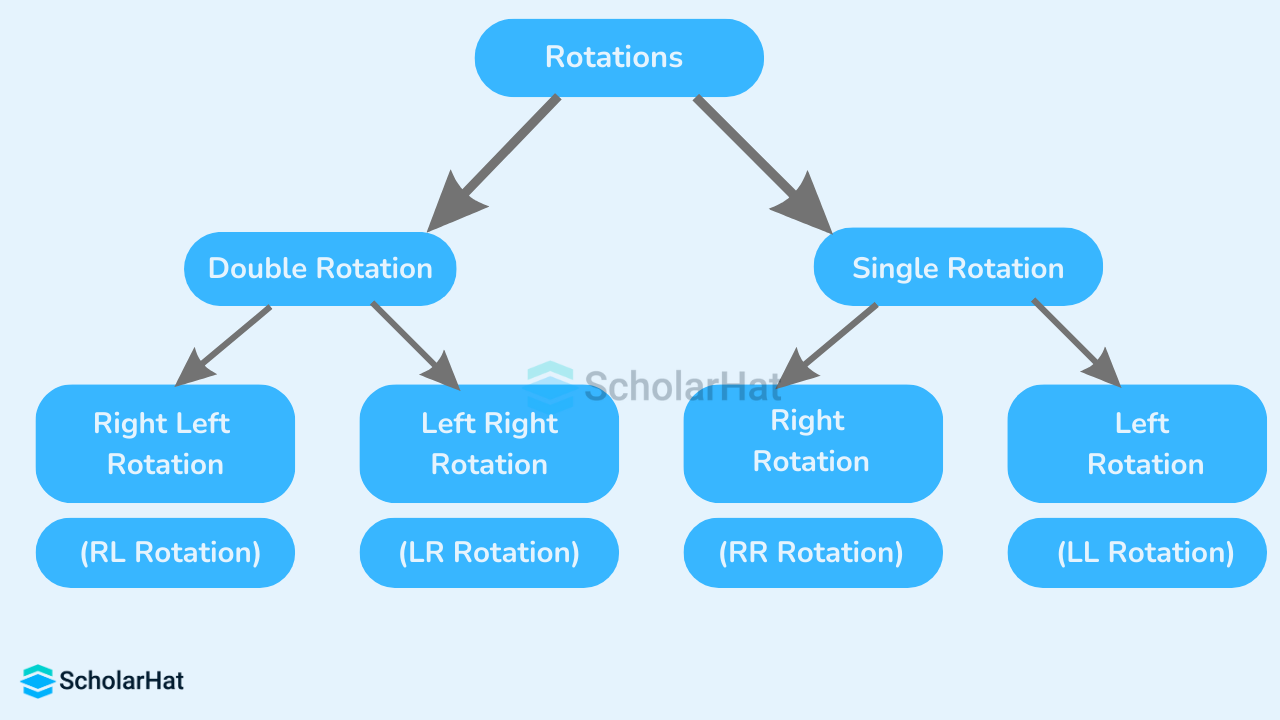
AVL Tree Rotations
AVL tree rotation is a fundamental operation used in self-balancing binary search trees, specifically in AVL trees. Due to any operations like insertion or deletion, if any node of an AVL tree becomes unbalanced, specific tree rotations are performed to restore the balance.The tree rotations involve rearranging the tree structure without changing the order of elements. The positions of the nodes of a subtree are interchanged. There are four types of AVL rotations:
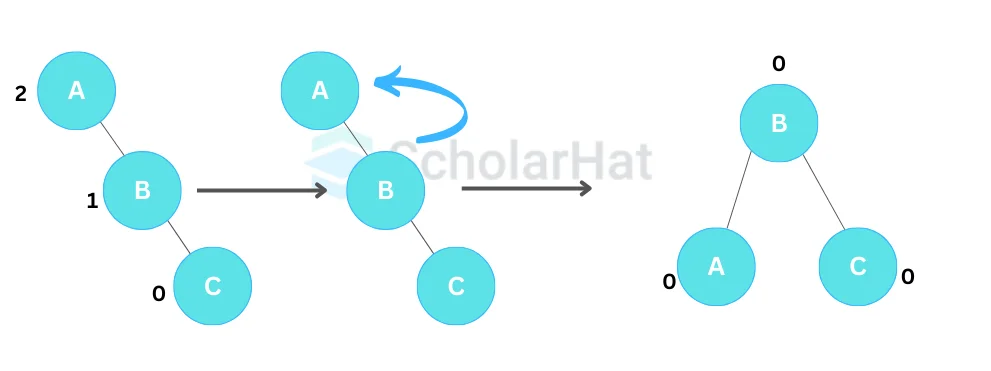
- Left Rotation (LL Rotation)
In a left rotation, a node's right child becomes the new root, while the original node becomes the left child of the new root. The new root's left child becomes the original node's right child.
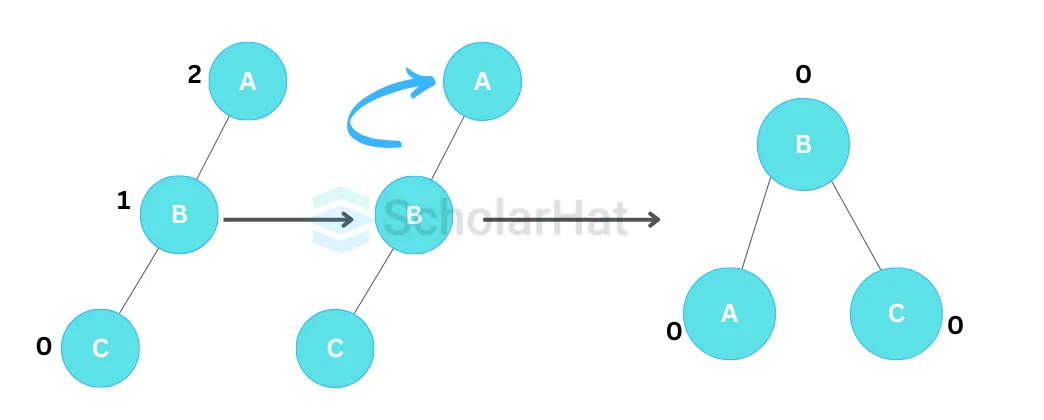
- Right Rotation (RR Rotation)
In a right rotation, a node's left child becomes the new root, while the original node becomes the right child of the new root. The new root's right child becomes the original node's left child.
- Left-Right Rotation (LR Rotation)
An LR rotation is a combination of a left rotation followed by a right rotation. It is performed when the left subtree of a node is unbalanced to the right, and the right subtree of the left child of that node is unbalanced to the left.
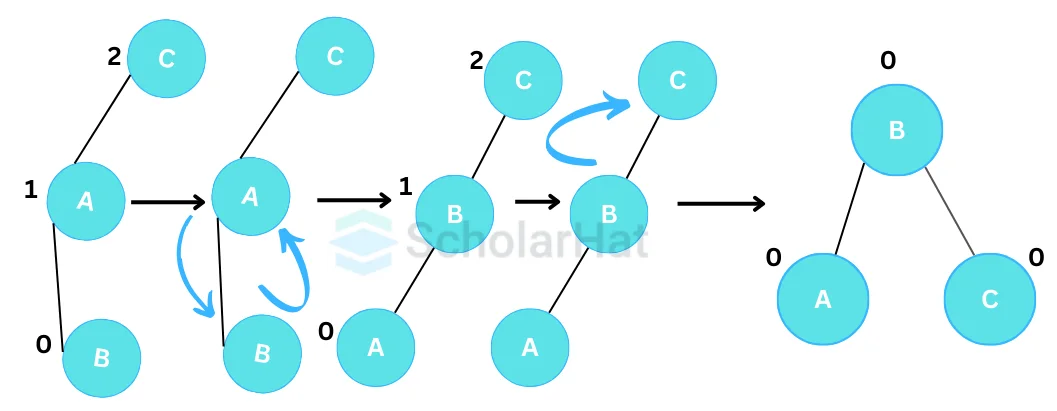
- Right-Left Rotation (RL Rotation)
An RL rotation is a combination of a right rotation followed by a left rotation. It is performed when the right subtree of a node is unbalanced to the left, and the left subtree of the right child of that node is unbalanced to the right.
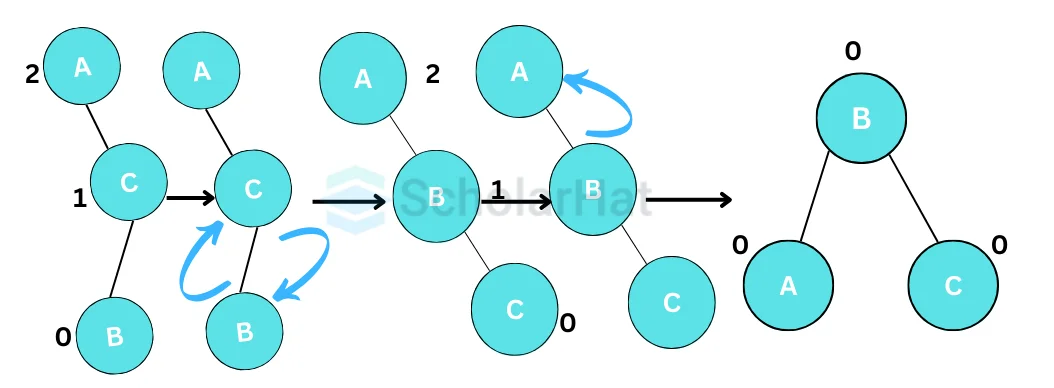
Read More - Data Structure Interview Questions for Experienced
Standard Operations on AVL Trees in Data Structures
- Insertion: A
newNodeis always inserted as a leaf node with a balance factor equal to 0. After each insertion, the ancestors of the newly inserted node are examined because the insertion only affects their heights, potentially inducing an imbalance. This process of traversing the ancestors to find the unbalanced node is called retracing.Algorithm for Insertion in an AVL Tree
Step 1: START Step 2: Insert the node using BST insertion logic. Step 3: Calculate and check the balance factor of each node. Step 4: If the balance factor follows the AVL criterion, go to step 6. Step 5: Else, perform tree rotations according to the insertion done. Once the tree is balanced go to step 6. Step 6: END- Let the initial tree be:
Let the node to be inserted be: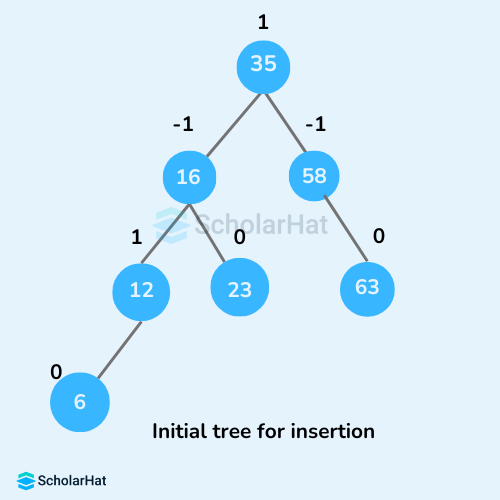
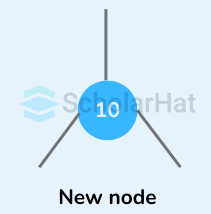
- Go to the appropriate leaf node to insert a
newNodeusing the following recursive steps. ComparenewKeywithrootKeyof the current tree.- If
newKey < rootKey, call the insertion algorithm on the left subtree of the current node until the leaf node is reached. - Else if
newKey > rootKey, call the insertion algorithm on the right subtree of the current node until the leaf node is reached. - Else, return
leafNode.
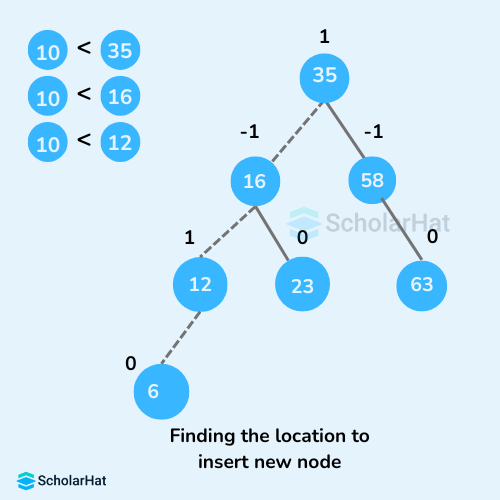
- If
- Compare
leafKeyobtained from the above steps withnewKey:- If
newKey<leafKey, makenewNodeas theleftChildofleafNode. - Else, make
newNodeasrightChildofleafNode.
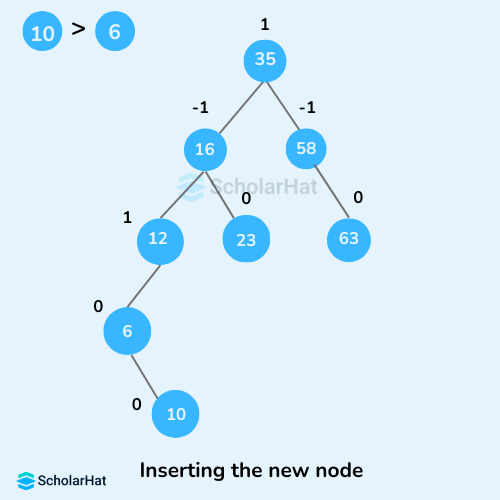
- If
- Update
balanceFactorof the nodes.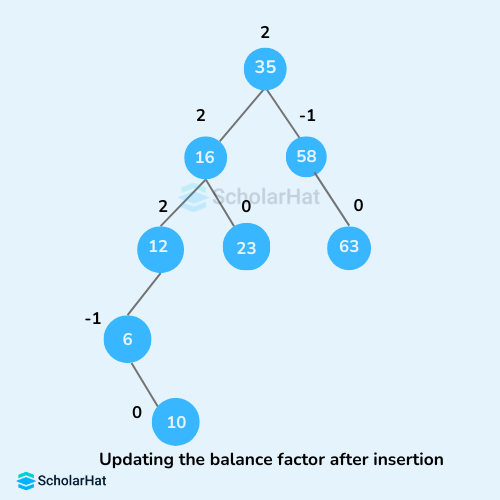
- If the nodes are unbalanced, then rebalance the node.
- If
balanceFactor > 1, which means the height of the left subtree is greater than that of the right subtree. So, do a right rotation or left-right rotation- If
newNodeKey < leftChildKeydo the right rotation. - Else, do left-right rotation.
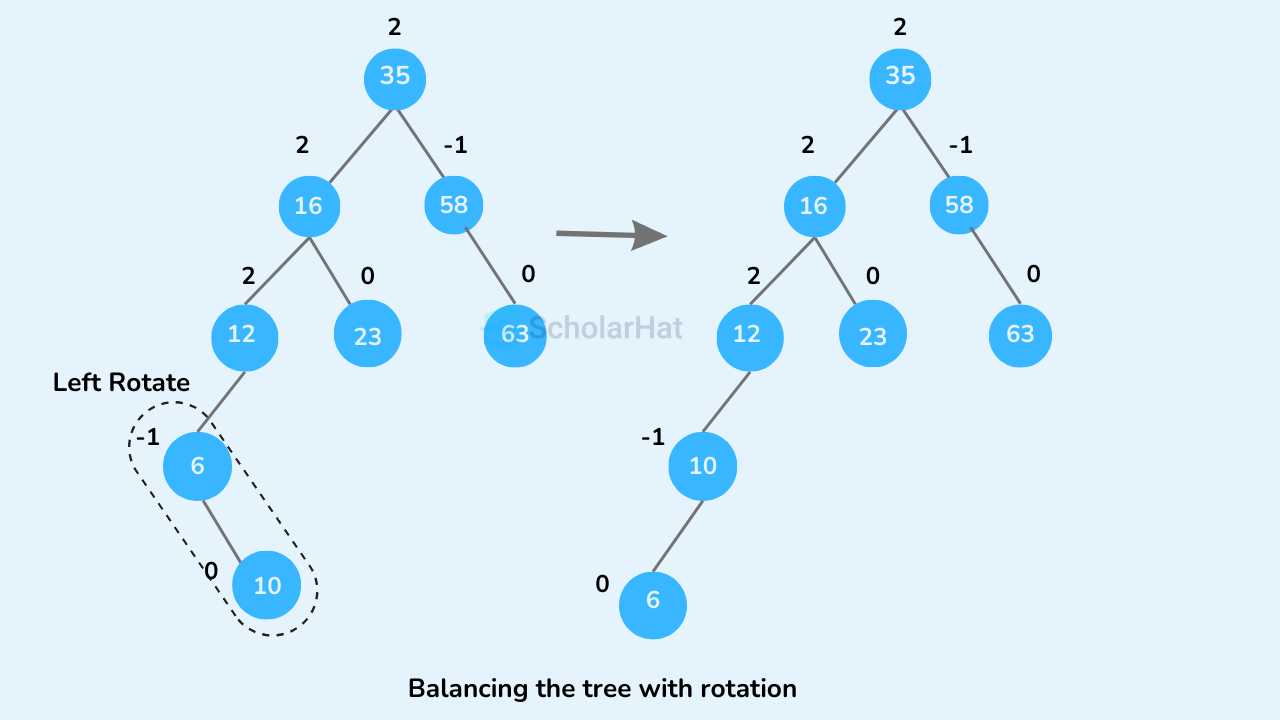
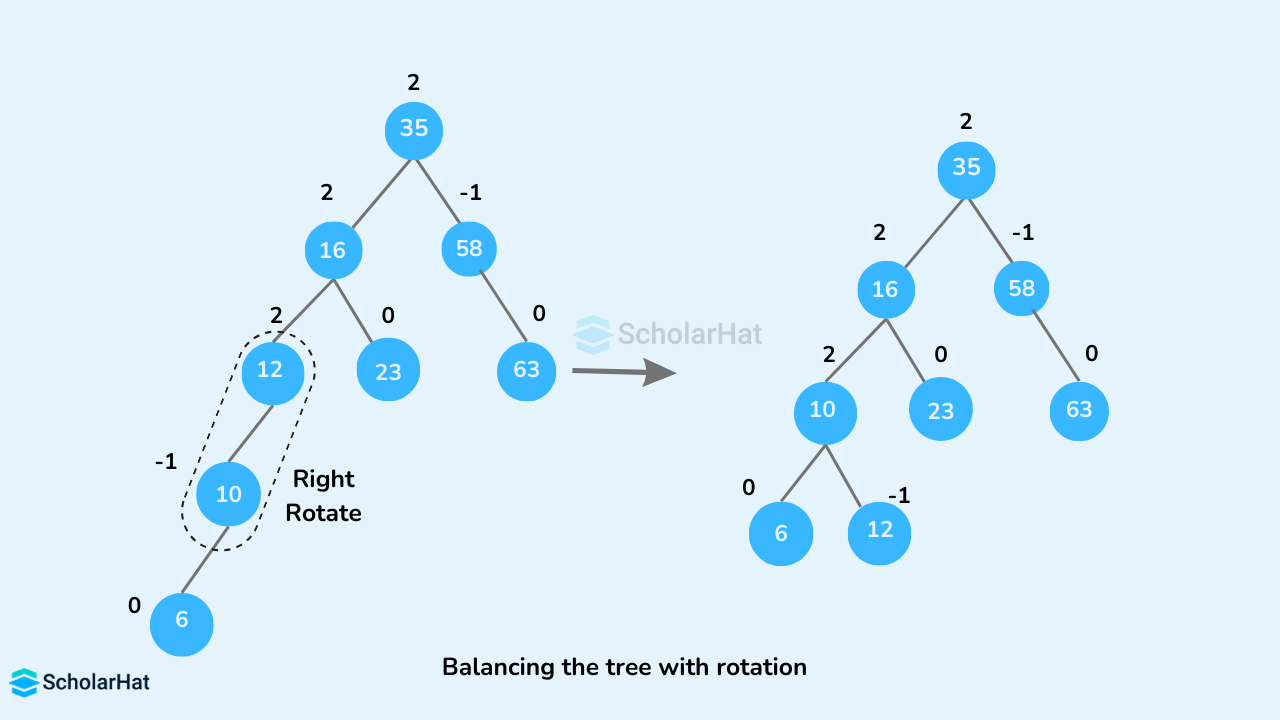
- If
- If
balanceFactor < -1, it means the height of the right subtree is greater than that of the left subtree. So, do a right rotation or right-left rotation- If
newNodeKey > rightChildKeydo a left rotation. - Else, do right-left rotation
- If
- If
- The final tree is:
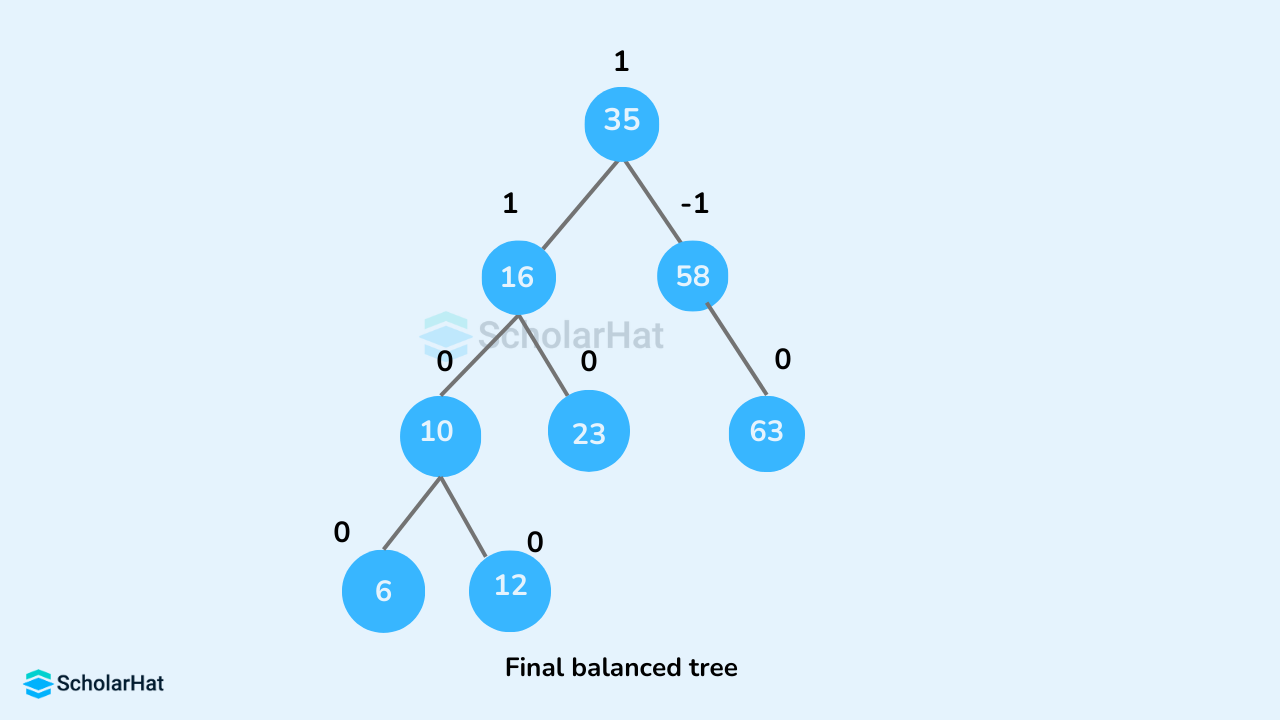
- Let the initial tree be:
- Deletion:A node is always deleted as a leaf node. After deleting a node, the balance factors of the nodes get changed. To rebalance the balance factor, suitable rotations are performed.
Algorithm for Deletion in an AVL Tree
Step 1: START Step 2: Find the node in the tree. If the element is not found, go to step 7. Step 3: Delete the node using BST deletion logic. Step 4: Calculate and check the balance factor of each node. Step 5: If the balance factor follows the AVL criterion, go to step 7. Step 6: Else, perform tree rotations to balance the unbalanced nodes. Once the tree is balanced go to step 7. Step 7: END- Locate
nodeToBeDeleted(recursion is used to findnodeToBeDeletedin the code used below).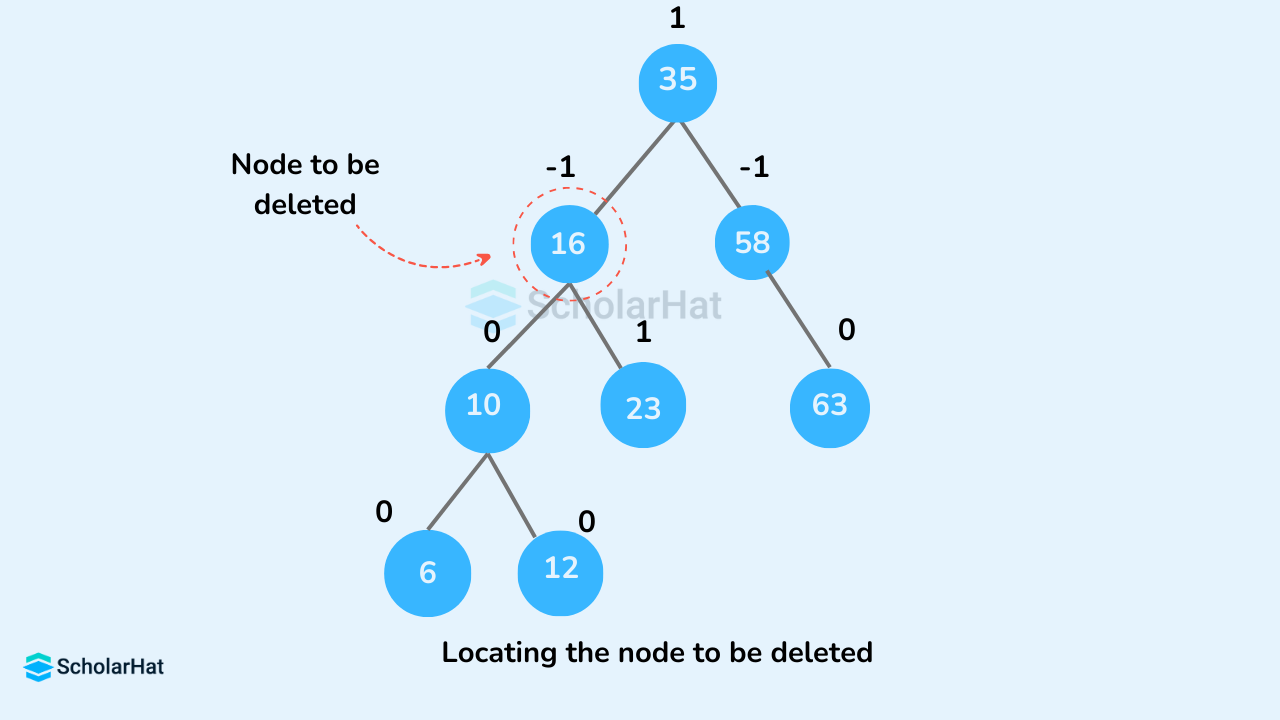
- There are three cases for deleting a node:
- If
nodeToBeDeletedis the leaf node (ie. does not have any child), then removenodeToBeDeleted. - If
nodeToBeDeletedhas one child, then substitute the contents ofnodeToBeDeletedwith that of the child. Remove the child. - If
nodeToBeDeletedhave two children, find the in-order successorwofnodeToBeDeleted(ie. node with a minimum value of key in the right subtree).
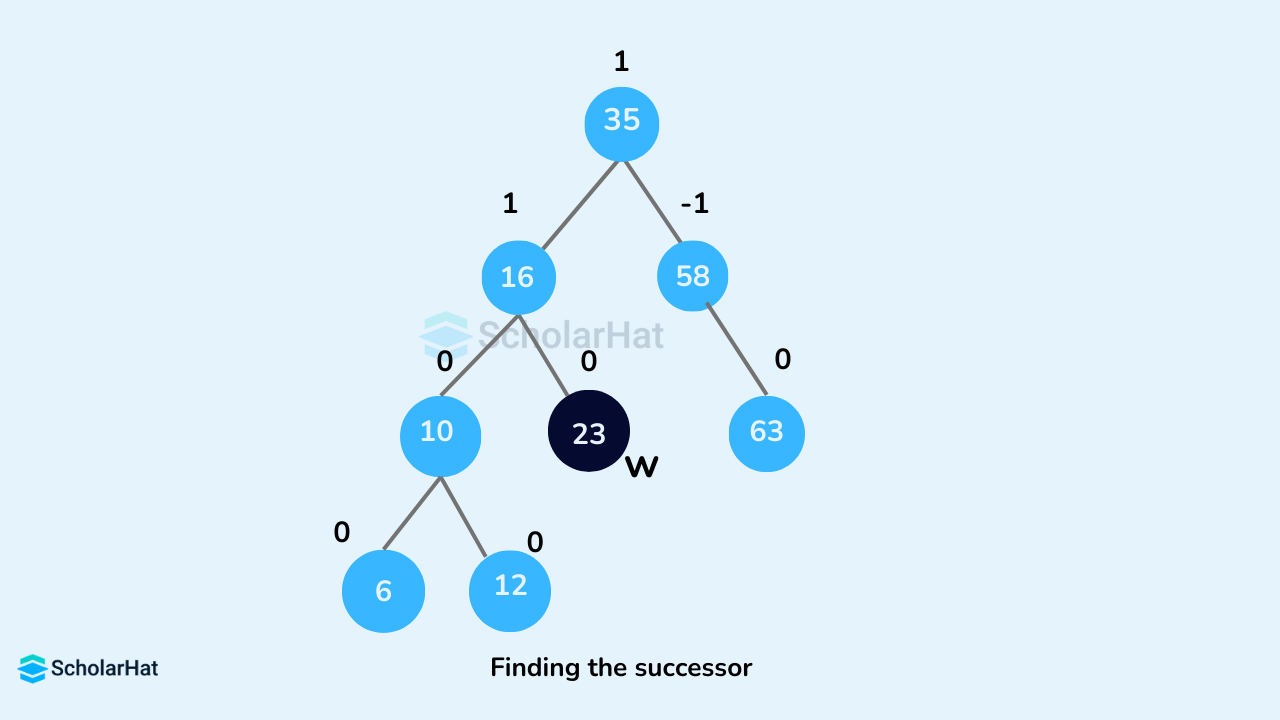
- Substitute the contents of
nodeToBeDeletedwith that ofw.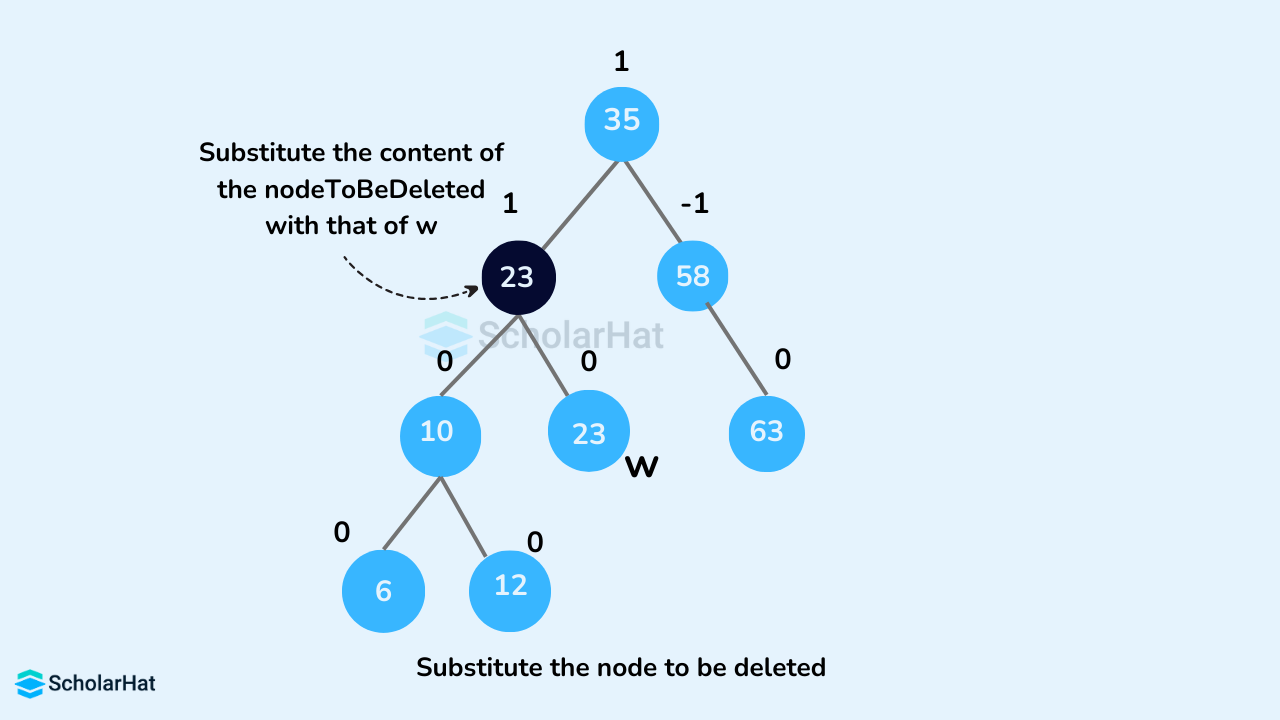
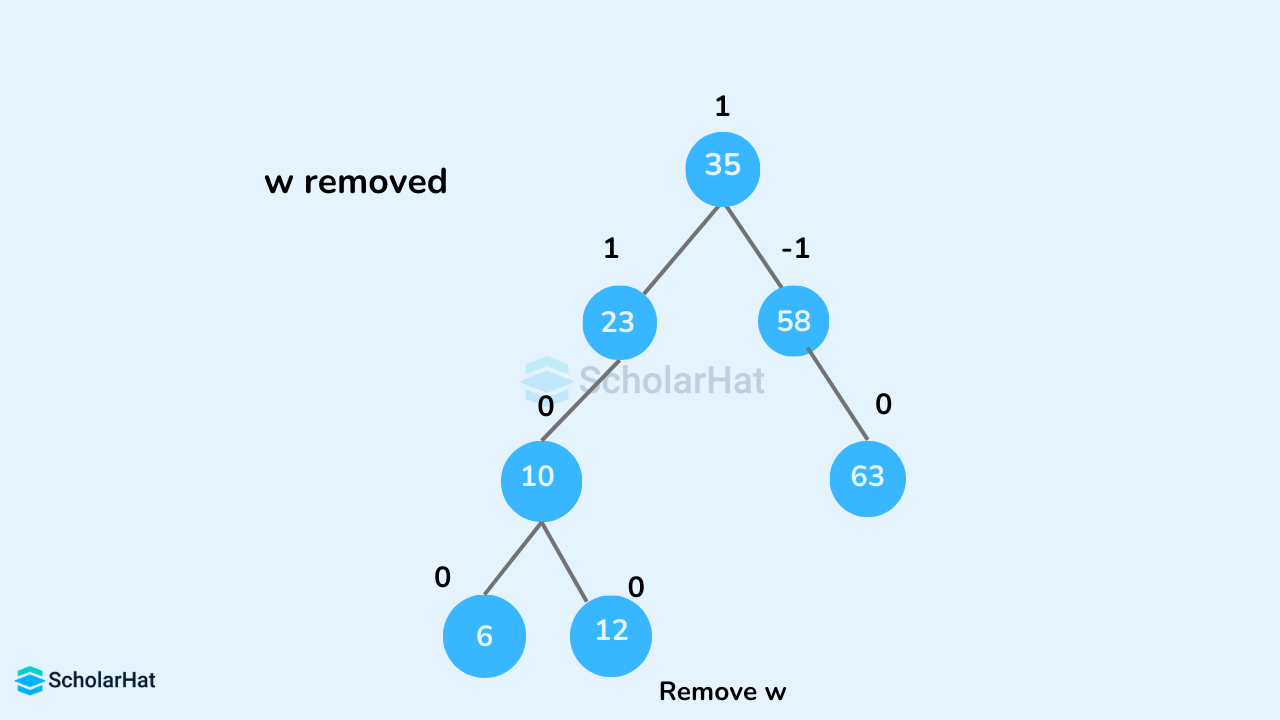
- Remove the leaf node
w.
- If
- Update
balanceFactorof the nodes.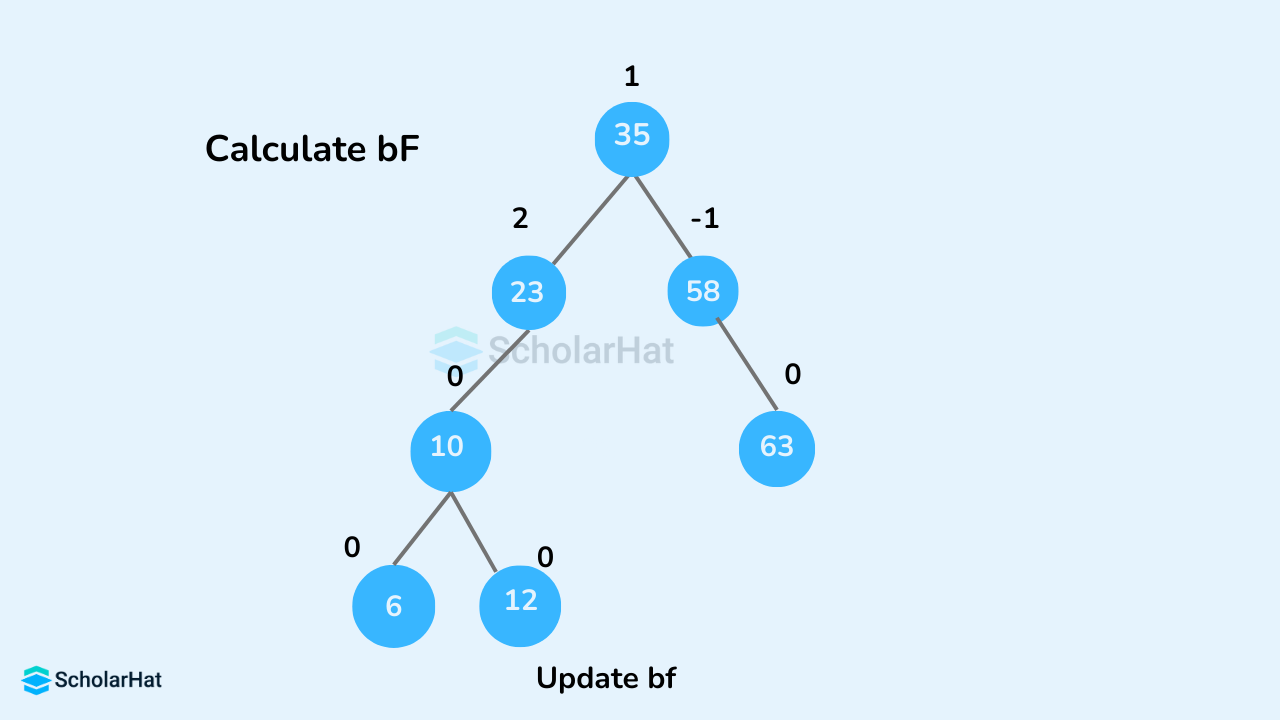
- Rebalance the tree if the balance factor of any of the nodes is not equal to -1, 0, or 1.
- If
balanceFactorofcurrentNode > 1,- If
balanceFactorofleftChild>= 0, do right rotation.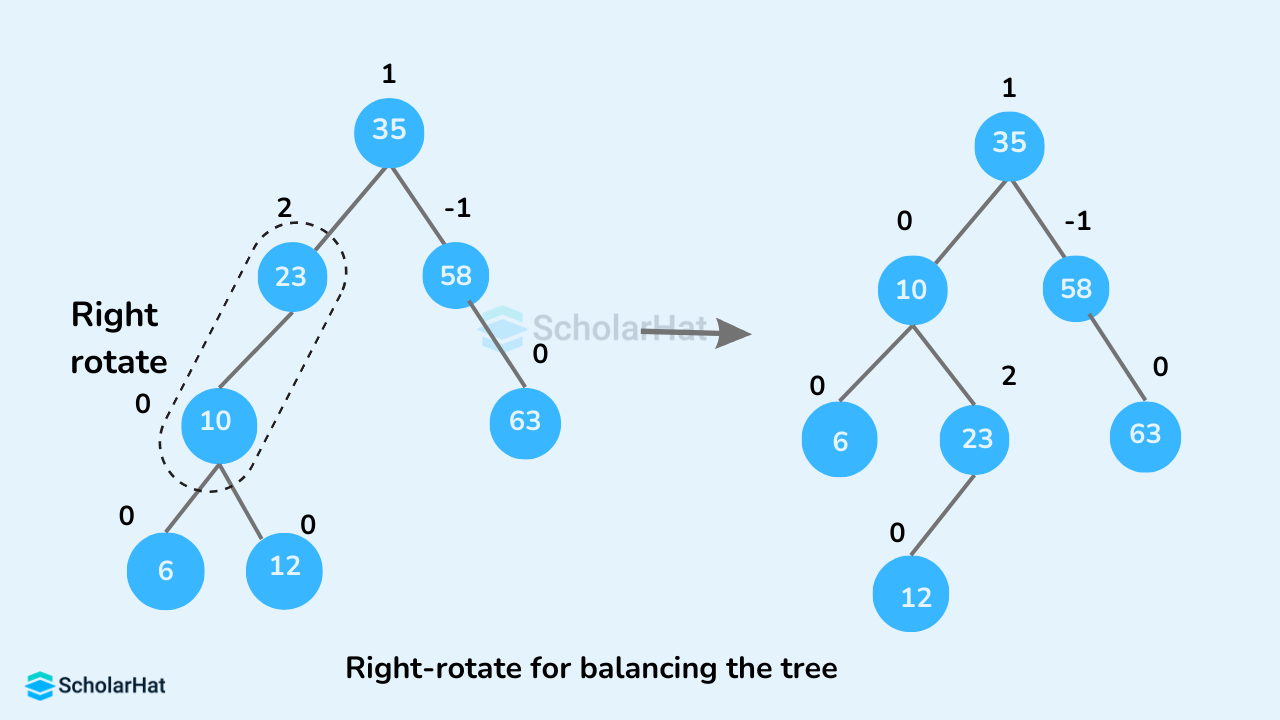
- Else do left-right rotation.
- If
- If
balanceFactorofcurrentNode< -1,- If
balanceFactorofrightChild<= 0, do left rotation. - Else do right-left rotation.
- If
- If
- The final tree is:
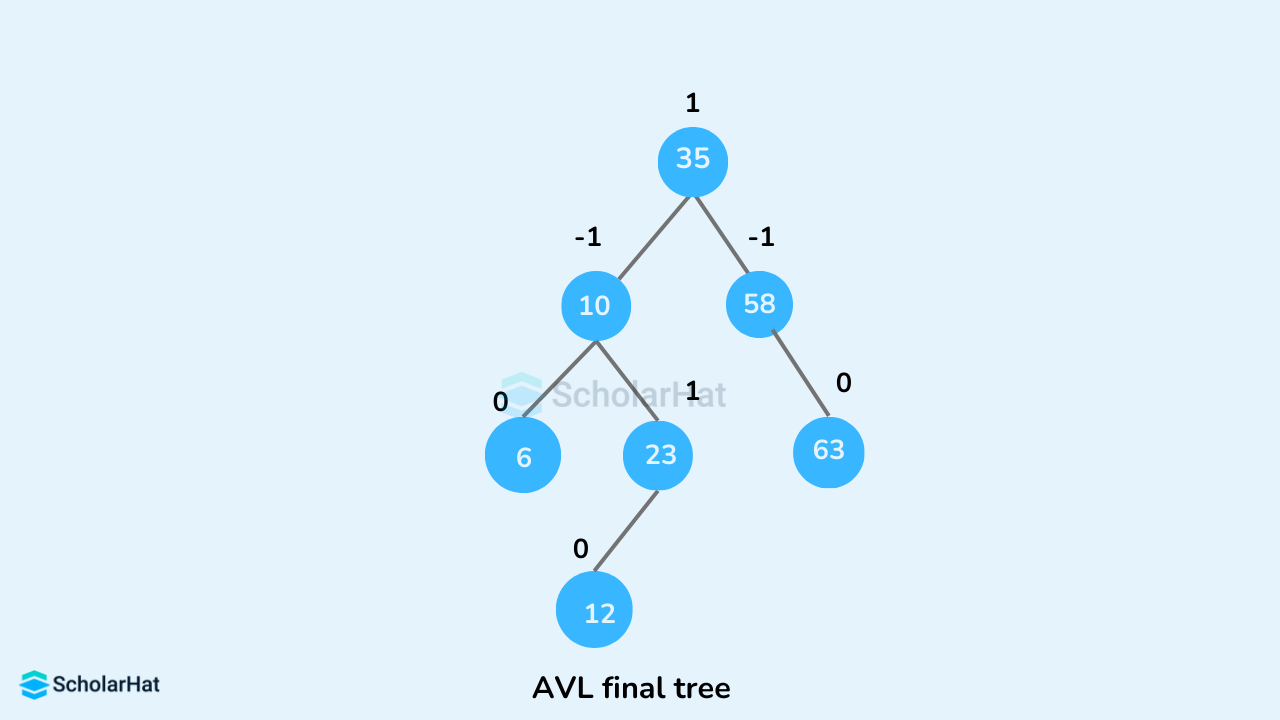
- Locate
Implementation of AVL Tree in Different Programming Languages
import sys
# Create a tree node
class TreeNode(object):
def __init__(self, key):
self.key = key
self.left = None
self.right = None
self.height = 1
class AVLTree(object):
# Function to insert a node
def insert_node(self, root, key):
# Find the correct location and insert the node
if not root:
return TreeNode(key)
elif key < root.key:
root.left = self.insert_node(root.left, key)
else:
root.right = self.insert_node(root.right, key)
root.height = 1 + max(self.getHeight(root.left),
self.getHeight(root.right))
# Update the balance factor and balance the tree
balanceFactor = self.getBalance(root)
if balanceFactor > 1:
if key < root.left.key:
return self.rightRotate(root)
else:
root.left = self.leftRotate(root.left)
return self.rightRotate(root)
if balanceFactor < -1:
if key > root.right.key:
return self.leftRotate(root)
else:
root.right = self.rightRotate(root.right)
return self.leftRotate(root)
return root
# Function to delete a node
def delete_node(self, root, key):
# Find the node to be deleted and remove it
if not root:
return root
elif key < root.key:
root.left = self.delete_node(root.left, key)
elif key > root.key:
root.right = self.delete_node(root.right, key)
else:
if root.left is None:
temp = root.right
root = None
return temp
elif root.right is None:
temp = root.left
root = None
return temp
temp = self.getMinValueNode(root.right)
root.key = temp.key
root.right = self.delete_node(root.right,
temp.key)
if root is None:
return root
# Update the balance factor of nodes
root.height = 1 + max(self.getHeight(root.left),
self.getHeight(root.right))
balanceFactor = self.getBalance(root)
# Balance the tree
if balanceFactor > 1:
if self.getBalance(root.left) >= 0:
return self.rightRotate(root)
else:
root.left = self.leftRotate(root.left)
return self.rightRotate(root)
if balanceFactor < -1:
if self.getBalance(root.right) <= 0:
return self.leftRotate(root)
else:
root.right = self.rightRotate(root.right)
return self.leftRotate(root)
return root
# Function to perform left rotation
def leftRotate(self, z):
y = z.right
T2 = y.left
y.left = z
z.right = T2
z.height = 1 + max(self.getHeight(z.left),
self.getHeight(z.right))
y.height = 1 + max(self.getHeight(y.left),
self.getHeight(y.right))
return y
# Function to perform right rotation
def rightRotate(self, z):
y = z.left
T3 = y.right
y.right = z
z.left = T3
z.height = 1 + max(self.getHeight(z.left),
self.getHeight(z.right))
y.height = 1 + max(self.getHeight(y.left),
self.getHeight(y.right))
return y
# Get the height of the node
def getHeight(self, root):
if not root:
return 0
return root.height
# Get balance factore of the node
def getBalance(self, root):
if not root:
return 0
return self.getHeight(root.left) - self.getHeight(root.right)
def getMinValueNode(self, root):
if root is None or root.left is None:
return root
return self.getMinValueNode(root.left)
def preOrder(self, root):
if not root:
return
print("{0} ".format(root.key), end="")
self.preOrder(root.left)
self.preOrder(root.right)
# Print the tree
def printHelper(self, currPtr, indent, last):
if currPtr != None:
sys.stdout.write(indent)
if last:
sys.stdout.write("R----")
indent += " "
else:
sys.stdout.write("L----")
indent += "| "
print(currPtr.key)
self.printHelper(currPtr.left, indent, False)
self.printHelper(currPtr.right, indent, True)
myTree = AVLTree()
root = None
nums = [22, 14, 72, 44, 25, 63, 98]
for num in nums:
root = myTree.insert_node(root, num)
myTree.printHelper(root, "", True)
key = 25
root = myTree.delete_node(root, key)
print("After Deletion: ")
myTree.printHelper(root, "", True)
// Create node
class Node {
int item, height;
Node left, right;
Node(int d) {
item = d;
height = 1;
}
}
// Tree class
class AVLTree {
Node root;
int height(Node N) {
if (N == null)
return 0;
return N.height;
}
int max(int a, int b) {
return (a > b) ? a : b;
}
Node rightRotate(Node y) {
Node x = y.left;
Node T2 = x.right;
x.right = y;
y.left = T2;
y.height = max(height(y.left), height(y.right)) + 1;
x.height = max(height(x.left), height(x.right)) + 1;
return x;
}
Node leftRotate(Node x) {
Node y = x.right;
Node T2 = y.left;
y.left = x;
x.right = T2;
x.height = max(height(x.left), height(x.right)) + 1;
y.height = max(height(y.left), height(y.right)) + 1;
return y;
}
// Get balance factor of a node
int getBalanceFactor(Node N) {
if (N == null)
return 0;
return height(N.left) - height(N.right);
}
// Insert a node
Node insertNode(Node node, int item) {
// Find the position and insert the node
if (node == null)
return (new Node(item));
if (item < node.item)
node.left = insertNode(node.left, item);
else if (item > node.item)
node.right = insertNode(node.right, item);
else
return node;
// Update the balance factor of each node
// And, balance the tree
node.height = 1 + max(height(node.left), height(node.right));
int balanceFactor = getBalanceFactor(node);
if (balanceFactor > 1) {
if (item < node.left.item) {
return rightRotate(node);
} else if (item > node.left.item) {
node.left = leftRotate(node.left);
return rightRotate(node);
}
}
if (balanceFactor < -1) {
if (item > node.right.item) {
return leftRotate(node);
} else if (item < node.right.item) {
node.right = rightRotate(node.right);
return leftRotate(node);
}
}
return node;
}
Node nodeWithMinimumValue(Node node) {
Node current = node;
while (current.left != null)
current = current.left;
return current;
}
// Delete a node
Node deleteNode(Node root, int item) {
// Find the node to be deleted and remove it
if (root == null)
return root;
if (item < root.item)
root.left = deleteNode(root.left, item);
else if (item > root.item)
root.right = deleteNode(root.right, item);
else {
if ((root.left == null) || (root.right == null)) {
Node temp = null;
if (temp == root.left)
temp = root.right;
else
temp = root.left;
if (temp == null) {
temp = root;
root = null;
} else
root = temp;
} else {
Node temp = nodeWithMinimumValue(root.right);
root.item = temp.item;
root.right = deleteNode(root.right, temp.item);
}
}
if (root == null)
return root;
// Update the balance factor of each node and balance the tree
root.height = max(height(root.left), height(root.right)) + 1;
int balanceFactor = getBalanceFactor(root);
if (balanceFactor > 1) {
if (getBalanceFactor(root.left) >= 0) {
return rightRotate(root);
} else {
root.left = leftRotate(root.left);
return rightRotate(root);
}
}
if (balanceFactor < -1) {
if (getBalanceFactor(root.right) <= 0) {
return leftRotate(root);
} else {
root.right = rightRotate(root.right);
return leftRotate(root);
}
}
return root;
}
void preOrder(Node node) {
if (node != null) {
System.out.print(node.item + " ");
preOrder(node.left);
preOrder(node.right);
}
}
// Print the tree
private void printTree(Node currPtr, String indent, boolean last) {
if (currPtr != null) {
System.out.print(indent);
if (last) {
System.out.print("R----");
indent += " ";
} else {
System.out.print("L----");
indent += "| ";
}
System.out.println(currPtr.item);
printTree(currPtr.left, indent, false);
printTree(currPtr.right, indent, true);
}
}
public static void main(String[] args) {
AVLTree tree = new AVLTree();
tree.root = tree.insertNode(tree.root, 22);
tree.root = tree.insertNode(tree.root, 14);
tree.root = tree.insertNode(tree.root, 72);
tree.root = tree.insertNode(tree.root, 44);
tree.root = tree.insertNode(tree.root, 25);
tree.root = tree.insertNode(tree.root, 63);
tree.root = tree.insertNode(tree.root, 98);
System.out.println("Before Deletion: ");
tree.printTree(tree.root, "", true);
tree.root = tree.deleteNode(tree.root, 25);
System.out.println("After Deletion: ");
tree.printTree(tree.root, "", true);
}
}
#include <iostream>
using namespace std;
class Node {
public:
int key;
Node *left;
Node *right;
int height;
};
int max(int a, int b);
// Calculate height
int height(Node *N) {
if (N == NULL)
return 0;
return N->height;
}
int max(int a, int b) {
return (a > b) ? a : b;
}
// New node creation
Node *newNode(int key) {
Node *node = new Node();
node->key = key;
node->left = NULL;
node->right = NULL;
node->height = 1;
return (node);
}
// Rotate right
Node *rightRotate(Node *y) {
Node *x = y->left;
Node *T2 = x->right;
x->right = y;
y->left = T2;
y->height = max(height(y->left),
height(y->right)) +
1;
x->height = max(height(x->left),
height(x->right)) +
1;
return x;
}
// Rotate left
Node *leftRotate(Node *x) {
Node *y = x->right;
Node *T2 = y->left;
y->left = x;
x->right = T2;
x->height = max(height(x->left),
height(x->right)) +
1;
y->height = max(height(y->left),
height(y->right)) +
1;
return y;
}
// Get the balance factor of each node
int getBalanceFactor(Node *N) {
if (N == NULL)
return 0;
return height(N->left) -
height(N->right);
}
// Insert a node
Node *insertNode(Node *node, int key) {
// Find the correct postion and insert the node
if (node == NULL)
return (newNode(key));
if (key < node->key)
node->left = insertNode(node->left, key);
else if (key > node->key)
node->right = insertNode(node->right, key);
else
return node;
// Update the balance factor of each node and
// balance the tree
node->height = 1 + max(height(node->left),
height(node->right));
int balanceFactor = getBalanceFactor(node);
if (balanceFactor > 1) {
if (key < node->left->key) {
return rightRotate(node);
} else if (key > node->left->key) {
node->left = leftRotate(node->left);
return rightRotate(node);
}
}
if (balanceFactor < -1) {
if (key > node->right->key) {
return leftRotate(node);
} else if (key < node->right->key) {
node->right = rightRotate(node->right);
return leftRotate(node);
}
}
return node;
}
// Node with minimum value
Node *nodeWithMimumValue(Node *node) {
Node *current = node;
while (current->left != NULL)
current = current->left;
return current;
}
// Delete a node
Node *deleteNode(Node *root, int key) {
// Find the node and delete it
if (root == NULL)
return root;
if (key < root->key)
root->left = deleteNode(root->left, key);
else if (key > root->key)
root->right = deleteNode(root->right, key);
else {
if ((root->left == NULL) ||
(root->right == NULL)) {
Node *temp = root->left ? root->left : root->right;
if (temp == NULL) {
temp = root;
root = NULL;
} else
*root = *temp;
free(temp);
} else {
Node *temp = nodeWithMimumValue(root->right);
root->key = temp->key;
root->right = deleteNode(root->right,
temp->key);
}
}
if (root == NULL)
return root;
// Update the balance factor of each node and
// balance the tree
root->height = 1 + max(height(root->left),
height(root->right));
int balanceFactor = getBalanceFactor(root);
if (balanceFactor > 1) {
if (getBalanceFactor(root->left) >= 0) {
return rightRotate(root);
} else {
root->left = leftRotate(root->left);
return rightRotate(root);
}
}
if (balanceFactor < -1) {
if (getBalanceFactor(root->right) <= 0) {
return leftRotate(root);
} else {
root->right = rightRotate(root->right);
return leftRotate(root);
}
}
return root;
}
// Print the tree
void printTree(Node *root, string indent, bool last) {
if (root != nullptr) {
cout << indent;
if (last) {
cout << "R----";
indent += " ";
} else {
cout << "L----";
indent += "| ";
}
cout << root->key << endl;
printTree(root->left, indent, false);
printTree(root->right, indent, true);
}
}
int main() {
Node *root = NULL;
root = insertNode(root, 22);
root = insertNode(root, 14);
root = insertNode(root, 72);
root = insertNode(root, 44);
root = insertNode(root, 25);
root = insertNode(root, 63);
root = insertNode(root, 98);
printTree(root, "", true);
root = deleteNode(root, 25);
cout << "After deleting " << endl;
printTree(root, "", true);
}
Output
R----44
L----22
| L----14
| R----25
R----72
L----63
R----98
After deleting
R----44
L----22
| L----14
R----72
L----63
R----98 Complexity Analysis of AVL Tree Operations
- Time Complexity:
Operations Best Case Average Case Worst Case Insertion O (log n)O (log n)O (log n)Deletion O (log n)O (log n)O (log n)Traversal O (n)O (n)O (n)Search O (log n)O (log n)O (log n) - Space Complexity: Space complexity is the same as that of Binary Search Trees i.e.,
O(n)as AVL Trees don't modify the data itself.
Applications of AVL Trees
- It is used to index huge records in a database and also search in that efficiently.
- For all types of in-memory collections, including sets and dictionaries, AVL Trees are used.
- Database applications, where insertions and deletions are less common but frequent data lookups are necessary.
- Software that needs optimized search.
- It is applied in corporate areas and storyline games.
Advantages of AVL Trees
- AVL trees are capable of self-balancing.
- It cannot be skewed.
- Compared to Red-Black Trees, it offers faster lookups.
- Superior searching efficiency compared to other trees, such as the binary tree.
- Height is limited to
log(n), wherenis the number of nodes in the tree as a whole.
Disadvantages of AVL Trees
- Implementing it is challenging.
- Certain procedures have high constant factors.
- Compared to Red-Black trees, AVL trees are less common.
- As additional rotations are conducted, AVL trees offer complex insertion and removal procedures because of their rather rigid balance.
- Requires to process more for balancing.
Summary
AVL Trees are a great tool to help structure and organize data. By keeping track of the difference in heights between two nodes, AVL trees can save you from calculating these values manually. Furthermore, as it is self-balancing, you need not worry about the tree becoming unbalanced as it grows. While traversing may take longer due to all the re-balancing, this method gives you greater control over your data sets than many regular BSTs.Top developers are already moving into Solution Architect roles. If you stay just a “coder,” you’ll be stuck while they lead. Enroll now in our Java Solution Architect Certification and step up.
FAQs
Take our Datastructures skill challenge to evaluate yourself!

In less than 5 minutes, with our skill challenge, you can identify your knowledge gaps and strengths in a given skill.












