What is a Graph in Data Structures and its Types?

A Graph in Data Structures is a type of non-primitive and non-linear data structure. A graph in data structure is a basic and adaptable structure that is used to show relationships between pairs of elements. It is made up of directed and/or undirected edges joining nodes, also known as vertices. When solving real-world issues like social networks, network connections, and route optimization, graphs are crucial. They play a vital role in both theoretical and practical applications because they support a wide range of algorithms for tasks including searching, shortest path finding, and cycle recognition.

In this DSA tutorial, we’ll explore the basics of graphs, including their features, types, and implementation methods. To deepen your understanding of graphs and other core data structure concepts, consider enrolling in our Data Structures and Algorithms (DSA) course. This course provides in-depth explanations, hands-on coding practice, and expert guidance to help you excel in technical interviews and solve complex real-world problems effectively.

What is a Graph in Data Structures?

• A graph is a collection of nodes that consist of data and are connected to other nodes of the graph.
• A Graph G=(V, E) is an ordered pair of two sets: V is called the Vertex set, and E is called the Edge set.
• Each edge in E is identified with a 2-vertex set of V:
• e-{u,v} means there is an edge from u to v and also from v to u.
• e-(u,v) means that there is an edge only from u to v.
• The most common real-life examples of graphs are social media, where a User, Photo, Album, Event, Group, Page, Comment, Story, Video, etc, represents a node.
• Every relationship is an edge from one node to another.
• Whenever you post a photo, join a group, like a page, etc., a new edge is created for that relationship.
• Thus, it can be said that a social media platform is a collection of nodes and edges.

Read More - Best Data Structure Interview Questions and Answers

Important Graph Terminologies:

1. Adjacent Vertices:

Vertices having a common edge are called Adjacent Vertices.

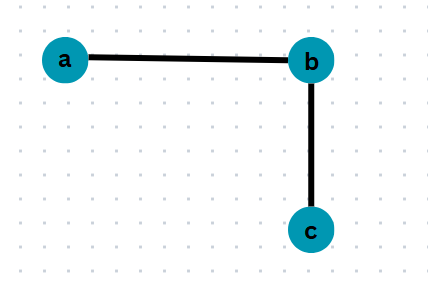
Here in this example, 

• a,b are adjacent vertices because there is an edge between them.
• b,c are adjacent vertices because there is an edge between them.
• a,c are not adjacent vertices because there is no edge between them.

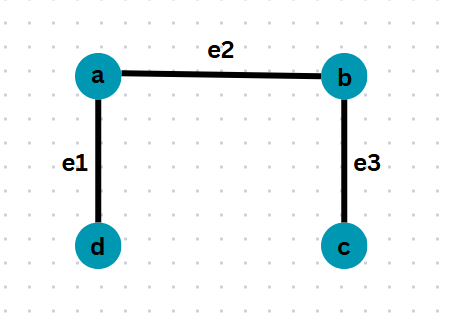
2. Adjacent Edges:

Edges having a common vertex are called adjacent edges.

Here in this example,

• e1,e2 are adjacent edges because they have vertex 'a' in common.
• e2,e3 are adjacent edges because they have vertex 'b' in common.
• e1,e3 are not adjacent edges because they have no vertex in common.

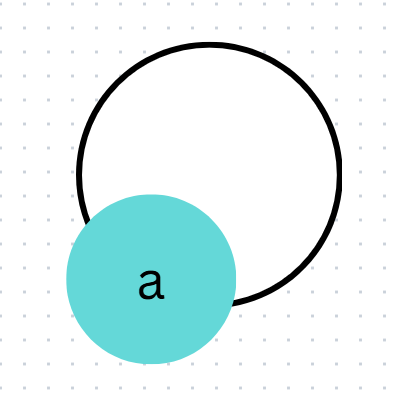
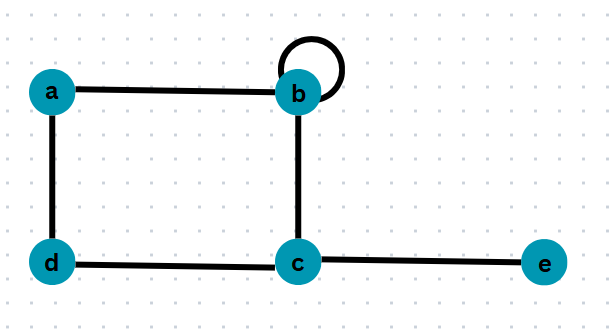
3. Self Loop:

An edge joining a vertex to itself.

Here in this example, there is an edge from vertex a to a. This is a self-loop.

4. Multi Edges:

If two or more edges join the same pairs of vertices, then those edges are called parallel edges or multiple edges.

Here in this example, three edges are connecting the same pair of vertices 'a' and 'b'. so these edges are parallel edges.

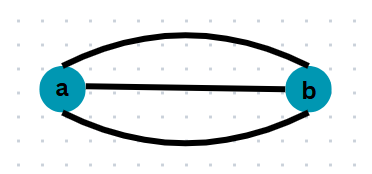
But here, there are no parallel edges because their directions are also mentioned.

5. Degree of a vertex:

• The number of edges incident on a vertex is called the degree of a vertex
• A self-loop is counted twice while counting the degree of vertices.
• The degree of a vertex is denoted by deg(v) or d(v).

Here in this graph, 

• The degree of vertex a is 2.
• The degree of vertex b is 4 (self-loop is counted twice).
• The degree of vertex c is 3.
• The degree of vertex d is 2.
• The degree of vertex e is 3 is 1.

6. Path:

A path is a sequence of connected edges that allows movement from one vertex to another within a graph. For example, in a graph structure, you can reach vertex 5 from vertex 3 either by following the path 3 → 4 → 5 or by taking the direct path 3 → 5.

Types of Graphs in Data Structures

1. Undirected Graph:

• G=(V, E), where each edge in E is represented by a set of two vertices {u,v} or {v,u} from V, is called an undirected graph.
• There is no specified direction in an undirected graph.
• If there is an edge from vertex1 to vertex2, then there is an edge from vertex2 to vertex1.

Example:

2. Directed Graph or Digraph:

• G=(V, E), where each edge e in E is defined by an ordered pair of two vertices (u, v) in V, is called a directed graph.
• If there is an edge from vertex1 to vertex2, there may or may not be an edge from vertex2 to vertex1.

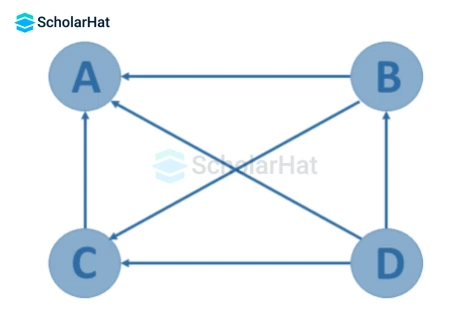
3. Simple Graph:

A Graph without Self-Loops and parallel edges is called a simple Graph. In Data structures, we only deal with Simple graphs and all the problems we solve are only related to simple graphs.

Example:

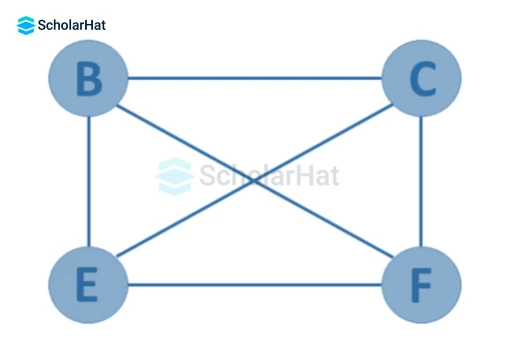
4. Multi Graph

A Multi Graph is a graph in which:

• Multi-edges or Parallel edges are allowed, but,
• Self-loop is not allowed.

Example:

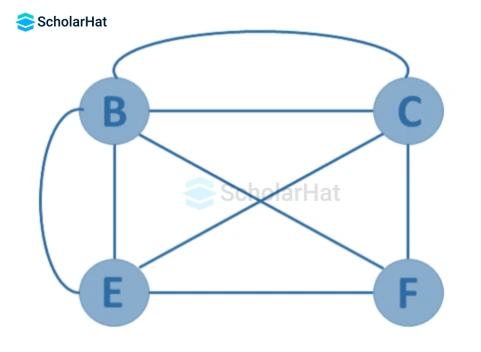
5. General Graph(Pseudo graph):

A Graph in which multiple edges and self-loops are allowed is called a general graph or a pseudo graph.

Example:

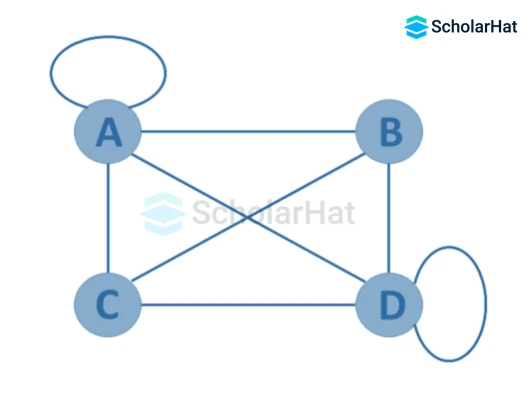
6. Finite Graph

If the graph, G=(V, E) has a finite number of edges and vertices, it is a finite graph. In other words, both the number of vertices and the number of edges in a finite graph are limited and can be counted.

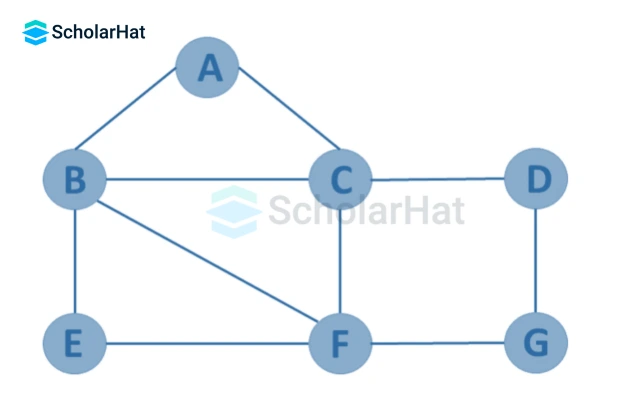
7. Infinite Graph

If the graph G=(V, E) has an infinite number of edges and vertices, it is an infinite graph.

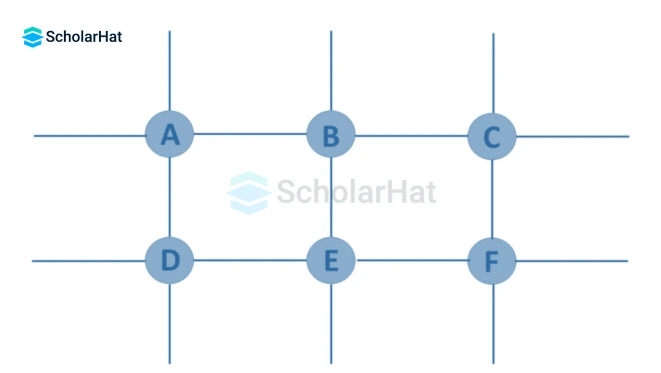
8. Trivial Graph

If a finite graph G=(V, E) has just one vertex and no edges, it is referred to as trivial. It is also known as a singleton graph or a single vertex graph.

9. Null Graph

It's a revised version of a trivial graph. A graph G=(V, E) is a null graph if it has many vertices, but none of them are connected by any edges. A null graph can also be referred to as an edgeless graph, an isolated graph, or a discrete graph.

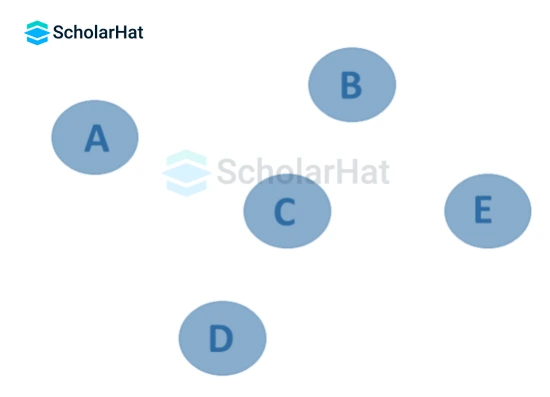
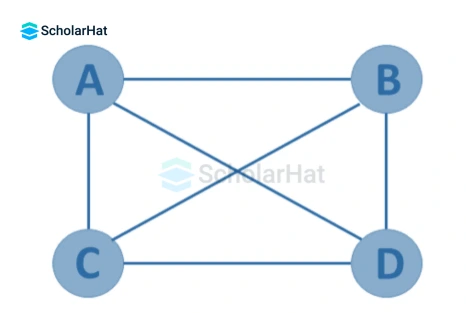
10. Complete Graph

A simple graph G=(V, E) with n vertices is also called a complete graph if the degree of each vertex is n-1, i.e. one vertex is attached with n-1 edges or the rest of the vertices in the graph. A complete graph is also called a Full Graph.

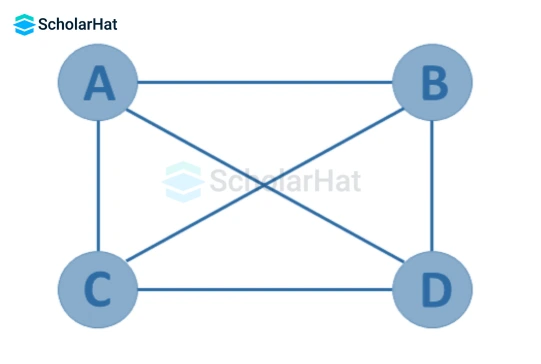
11. Regular Graph

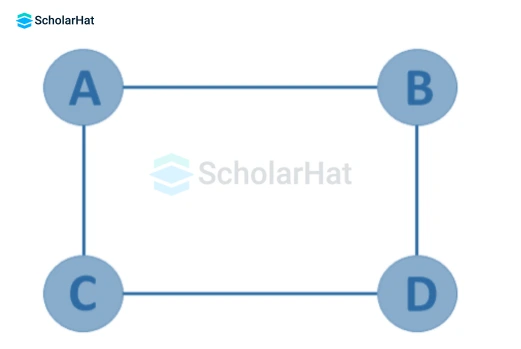
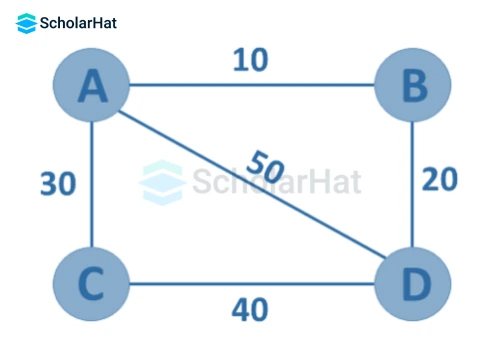
12. Weighted Graph

A graph G=(V, E) in which edges have weights or costs associated with them is a weighted graph.

13. Connected Graph

A graph G = (V, E) is said to be connected if there exists at least one path between each and every pair of vertices in the graph.

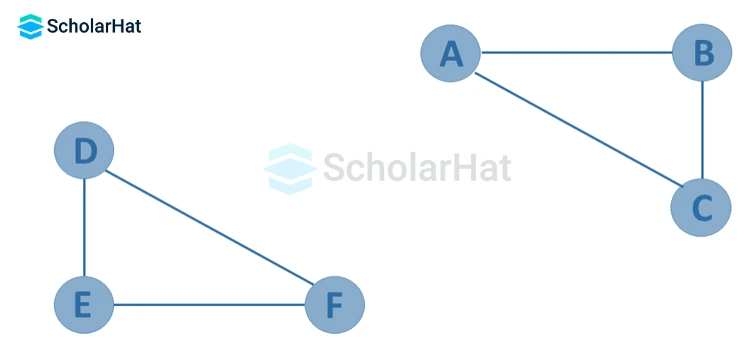
14. Disconnected Graph

If in a graph G = (V, E), there does not exist any path between at least one pair of vertices, it is a disconnected graph. A null graph with n vertices is a disconnected graph.

15. Cyclic Graph

A graph is termed cyclic if it forms at least one cycle.

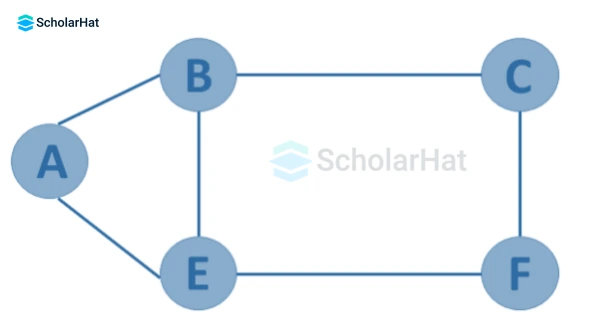
16. Acyclic Graph

A graph is said to be acyclic if it contains no cycles.

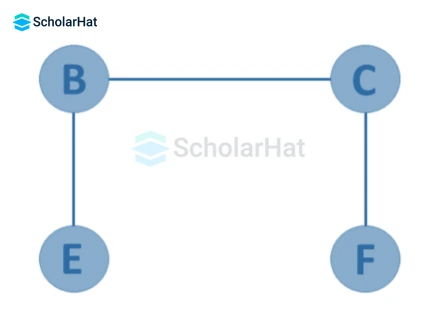
17. Directed Acyclic Graph

It is a graph with directed edges but no cycle.

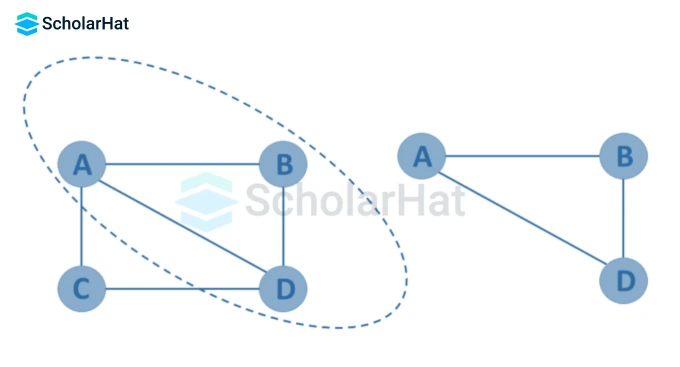
18. Subgraph

A subgraph is a set of vertices and edges in one graph that are subsets of another.

Graph Representation in Data Structures

• Graph representation is a way of structuring and visualizing data using nodes (vertices) and edges. It is also a technique for storing graphs in a computer's memory.
• In a graph, nodes represent individual entities, while edges represent the relationships or connections between those entities. Depending on whether the edges have a specific direction, the connections can be directional or undirected.

There are two ways to represent a graph

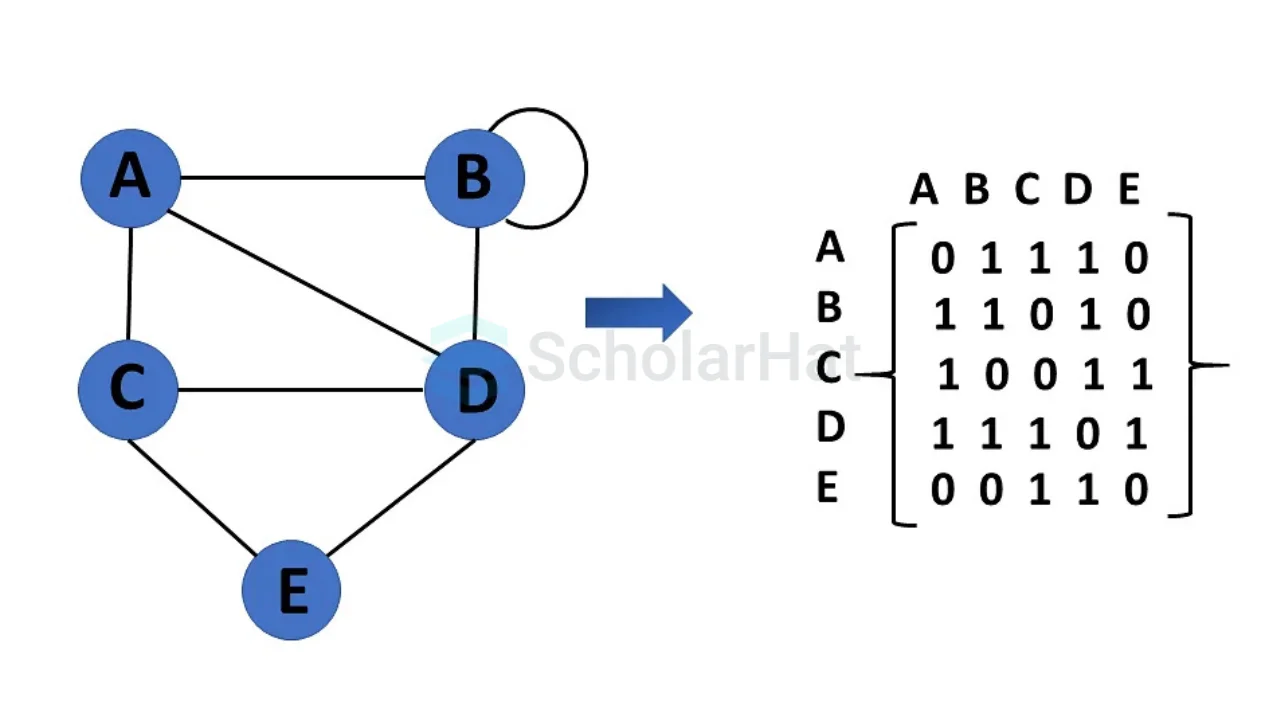
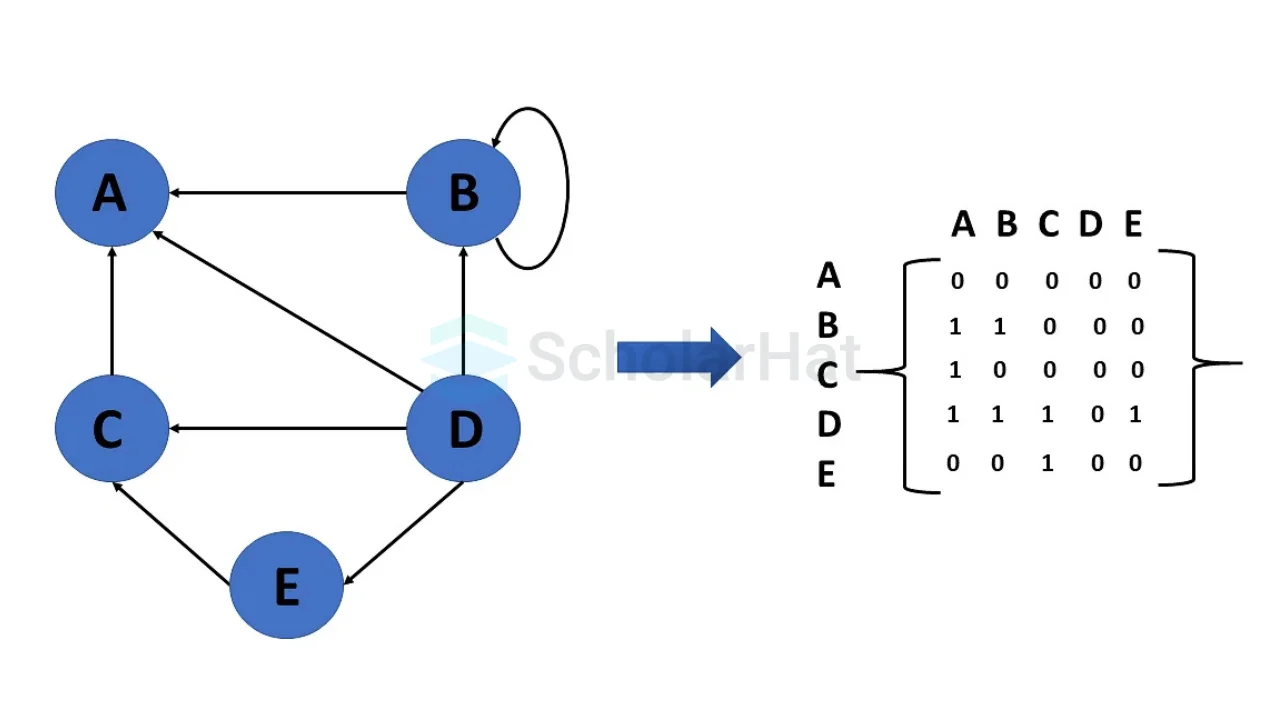
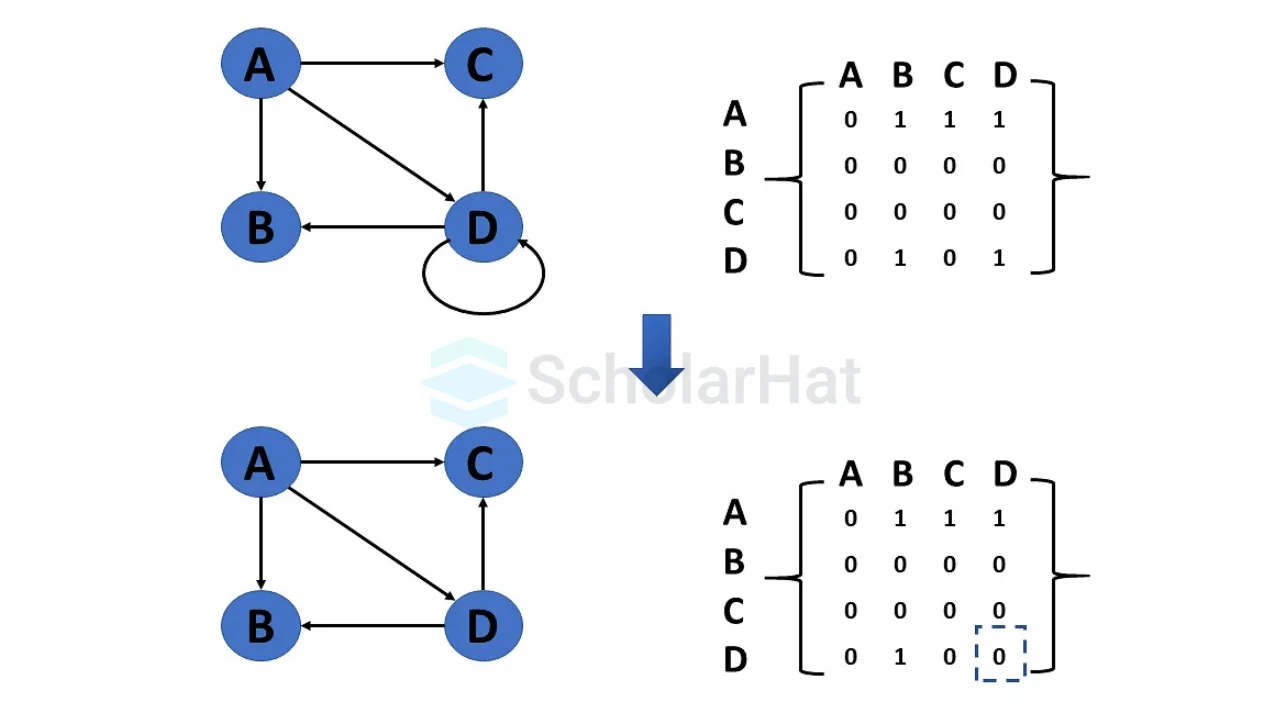
1. Adjacency Matrix

An adjacency matrix is a 2D array of size V × V, where V is the number of vertices (or nodes) in the graph. It is used to represent the connections between vertices. Each cell (i, j) in the matrix contains:

• 1 if there is an edge between vertex i and vertex j (in unweighted graphs).
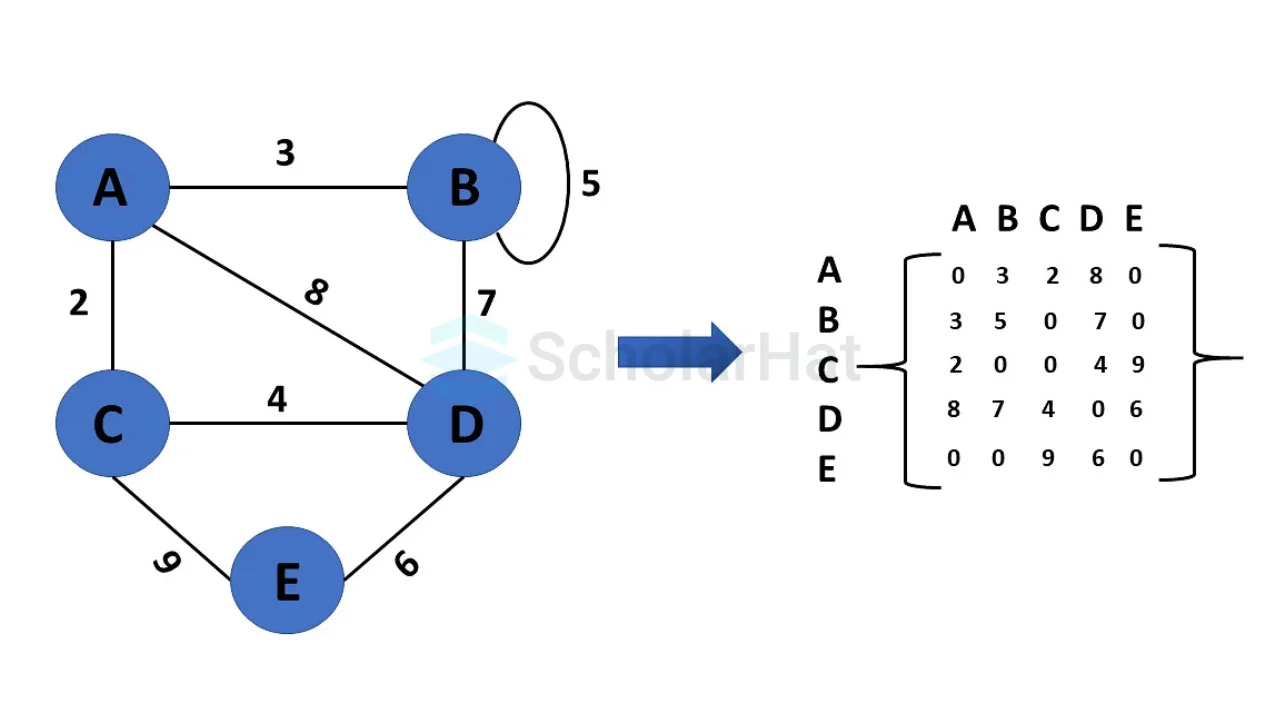
• A weight (like 5, 10, etc.) if the graph is weighted.
• 0 if there is no edge between i and j.

Since the matrix has the same number of rows and columns, it is a square matrix. The adjacency matrix makes it easy to check if two vertices are connected.

Representation of an Undirected Graph

Representation of a Directed Graph

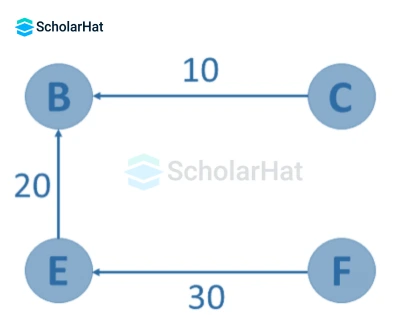
Weighted Undirected Graph Representation

A weighted graph representing these values in the matrix is indicated at the graph's edge.

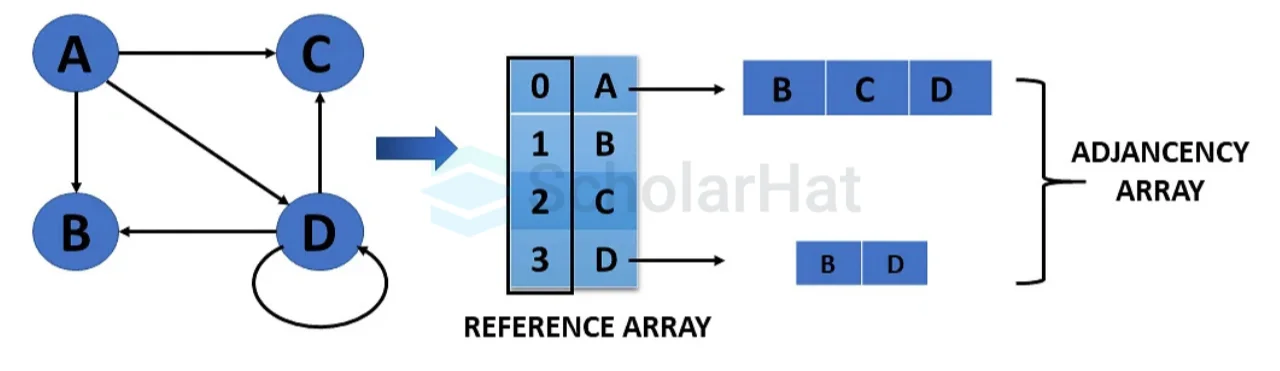
2. Adjacency List

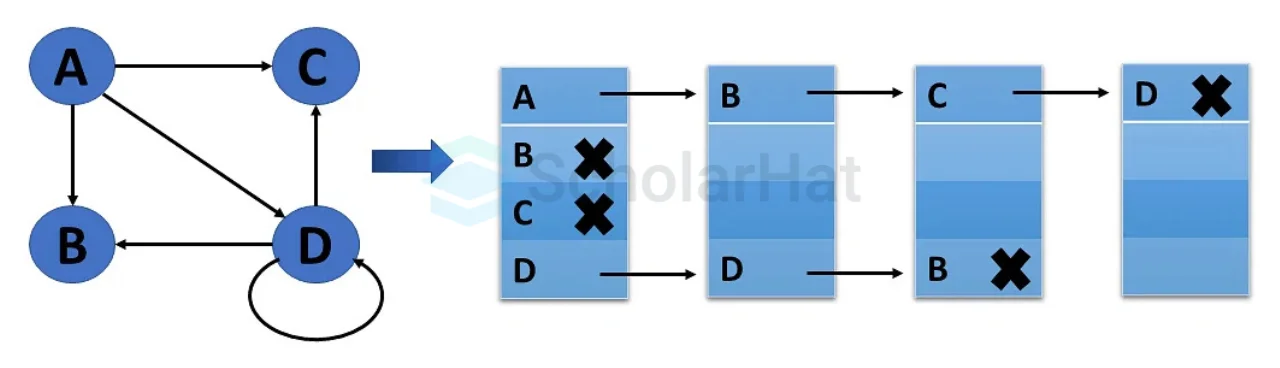
An adjacency list represents a graph as an array of linked lists. The index of the array represents a vertex and each element in its linked list represents the other vertices that form an edge with the vertex.

Weighted Undirected Graph Representation Using Linked-List

Weighted Undirected Graph Representation Using an Array

Operations on Graphs in Data Structures

The following common operations are performed on graphs in data structures:

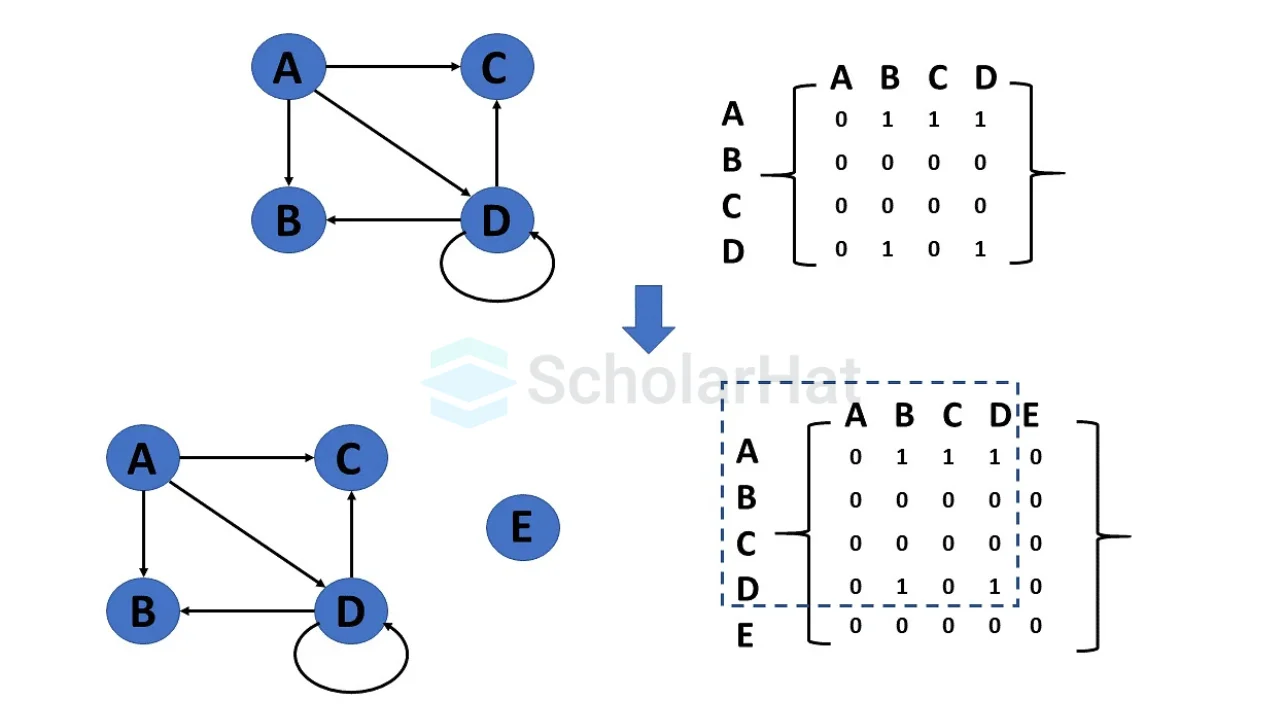
1. Insert vertex

It is a simple addition of a vertex(node) in a graph. It need not be connected to any other vertex(node) through an edge.

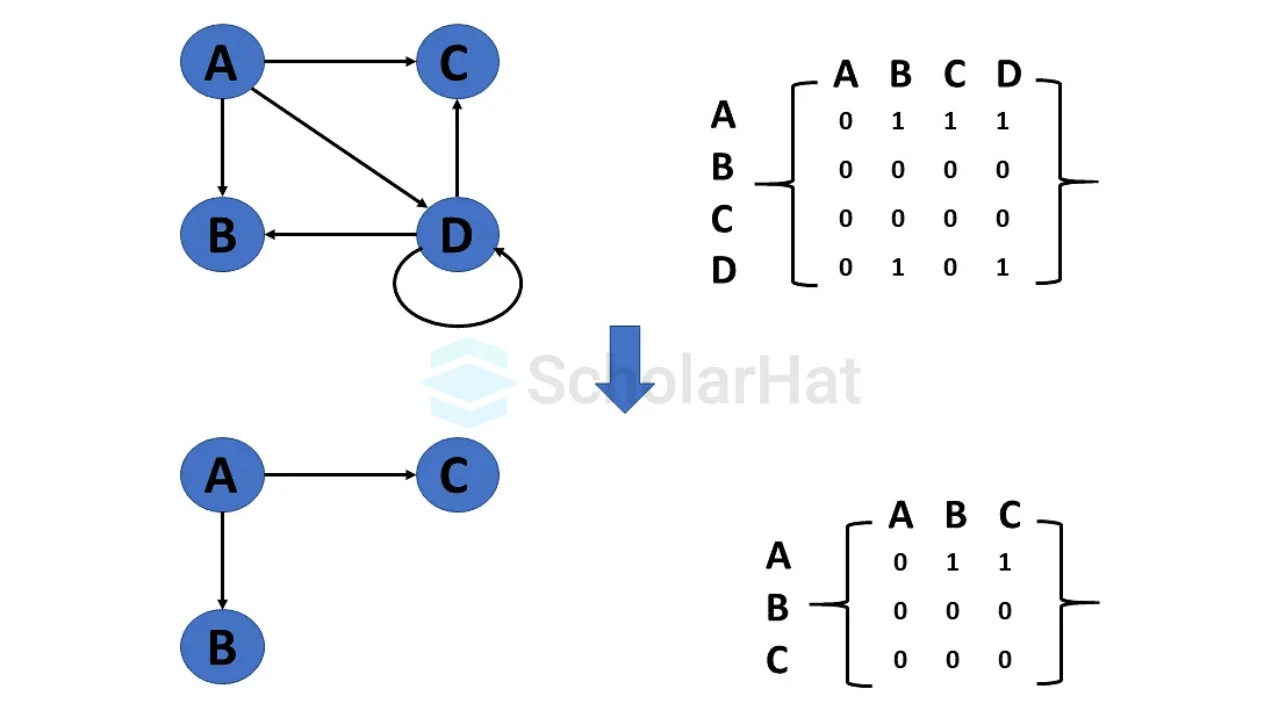
2. Delete vertex

To delete a nod, we also have to remove all the edges associated with that vertex.

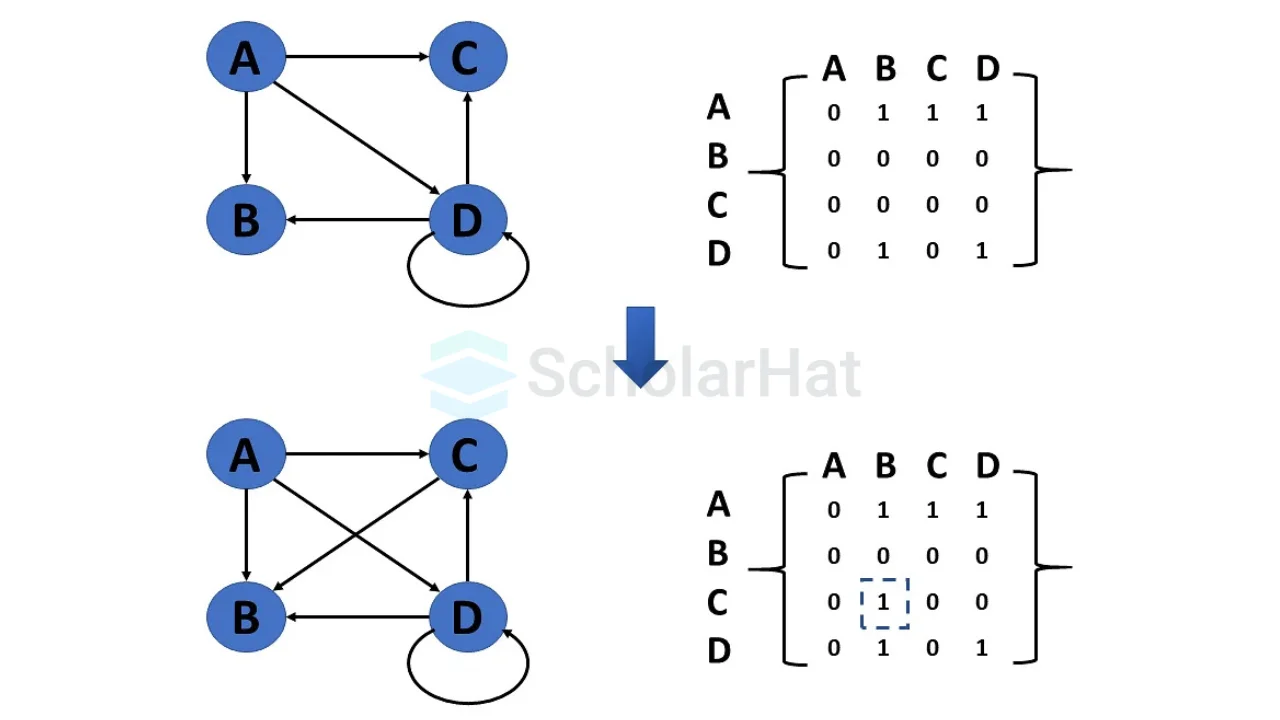
3. Insert Edge

It adds an edge between a pair of vertices.

4. Delete Edge

An edge can be deleted by severing the link between its vertices or nodes. If all the edges from a particular vertex(node) are removed, then that vertex(node) becomes an isolated vertex.

5. Graph Traversal

Graph traversal is the process of going through or updating each vertex in a graph. Such traversals are classified according to the order in which the algorithm visits the vertices. A subset of tree traversal is graph traversal.

There are two algorithms/ways to visit a graph:

1. Breadth-first search
2. Depth-first search

We will study all these two in the section Breadth First Traversal and Depth First Traversal

Application of Graphs

1. Maps GPS Systems can be represented using graphs and then can be used by computers to provide various services.
2. When various tasks depend on each other, it can be represented using a Directed Acyclic graph and we can find the order in which tasks can be performed using topological sort.
3. State Transition Diagram represents what can be the legal moves from current states.
4. Graphs can be used to represent the topology of computer networks, such as the connections between routers and switches.

Advantages of Graphs

1. Graphs can be used to represent a wide range of relationships and data structures.
2. They can be used to model and solve a wide range of problems, including pathfinding, data clustering, network analysis, and machine learning.
3. Graph algorithms are often very efficient and can be used to solve complex problems quickly and effectively.
4. They can be used to represent complex data structures simply and intuitively, making them easier to understand and analyze.

Disadvantages of Graphs

1. Graphs can be complex and difficult to understand, especially for people not familiar with graph theory or related algorithms.
2. Creating and manipulating graphs can be computationally expensive, especially very large or complex graphs.
3. Graph algorithms can be difficult to design and implement correctly and can be prone to bugs and errors.
4. Graphs can be difficult to visualize and analyze, especially for very large or complex graphs, which can make it challenging to extract meaningful insights from the data.

Summary

In this article, we explored the fundamentals of graphs in data structures, including their definition, key terminologies, types, representations, and operations. We learned how graphs are used to model relationships and solve real-world problems such as network routing, social connections, and task scheduling. We also covered graph traversal methods and discussed both the advantages and challenges of using graphs. Mastering graphs is essential for effective problem-solving and success in technical interviews and advanced algorithm design.

To further enhance your understanding and application of graph concepts, consider enrolling in the Free DSA Certification Course, where you can gain comprehensive insights into effective data structure utilization for improved problem-solving and time management.

Take our Datastructures skill challenge to evaluate yourself!

In less than 5 minutes, with our skill challenge, you can identify your knowledge gaps and strengths in a given skill.

GET FREE CHALLENGE