28
DecStack in Data Structures: Implementations in Java, Python, & C++
A stack in data structures is a linear collection that follows the Last In, First Out (LIFO) principle, where the last element added is the first to be removed. This structure is essential in various algorithms and applications such as expression evaluation, backtracking, and memory management. Stack implementation can be done using different programming languages such as stack in data structures using C, and stack in data structures using Java etc.
In this DSA tutorial, you will able to know about Stack in data structure, Standard Operations on stack, Working of Stack in Data Structures, Implementation of Stack in Different Programming Languages, Applications of stack in data structure, further you will understand about Advantages and Disadvantages of Stack in data structure. DSA skills can boost your tech salary by 25% in 2025. Enroll in our Free DSA Course with Certificate today!
What is a Stack in Data Structures?
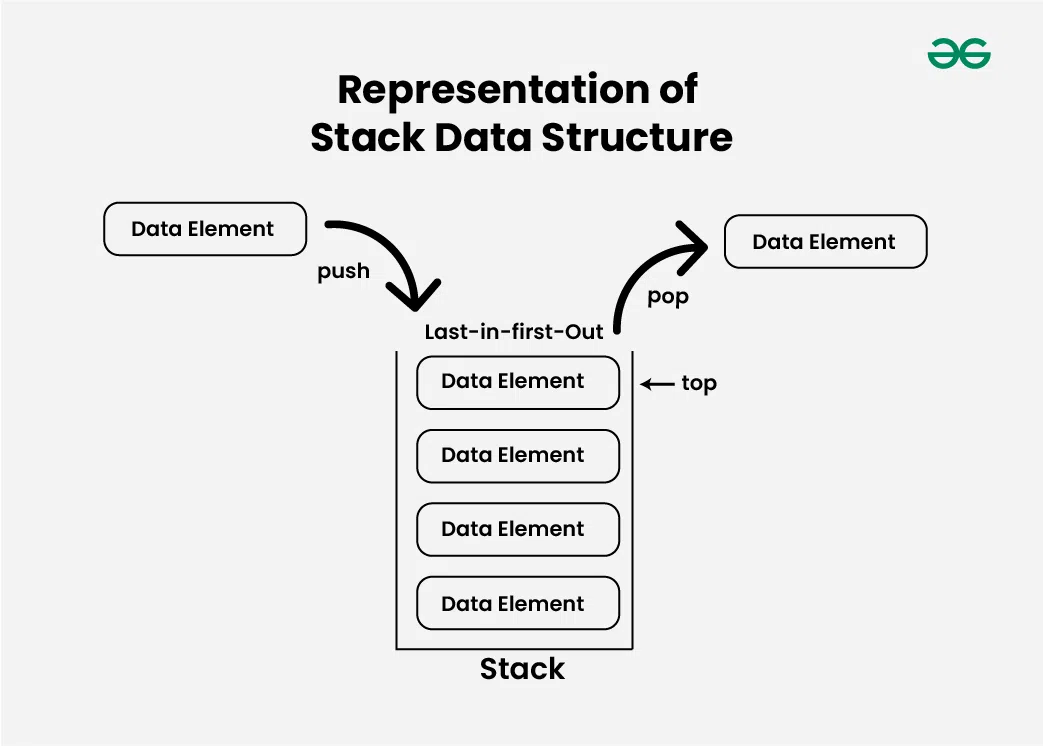
A Stack is a linear data structure that follows a particular order in which the operations are performed.
- One End Access: A stack is an ordered list or we can say a container in which insertion and deletion can be done from the one end known as the top of the stack.
- LIFO Order: The last inserted element is available first and is the first one to be deleted. Hence, it is known as Last In, First Out
LIFOor First In, Last OutFILO. - Top element: In a stack, the element at the top is known as the
topelement. When a new element is added to the stack, it is placed on top of the existing elements. - Stacks are dynamic; this means that they do not have a fixed size and their size can be increased or decreased depending upon the number of elements.
Real-World Examples:
1. Stack of Plates
- Plates are placed one on top of another.
- The last plate added (on top) is the first to be taken out.
2. Browser History (Back Button)
- When you visit a new webpage, it's pushed onto a history stack.
- Pressing the Back button pops the most recent page, showing the previous one.
3. Undo Feature in Text Editors
- Every action is pushed onto a stack.
- Pressing Undo pops the last action and reverses it.
Standard Operations on Stack
Let's see the basic operations in the stack.
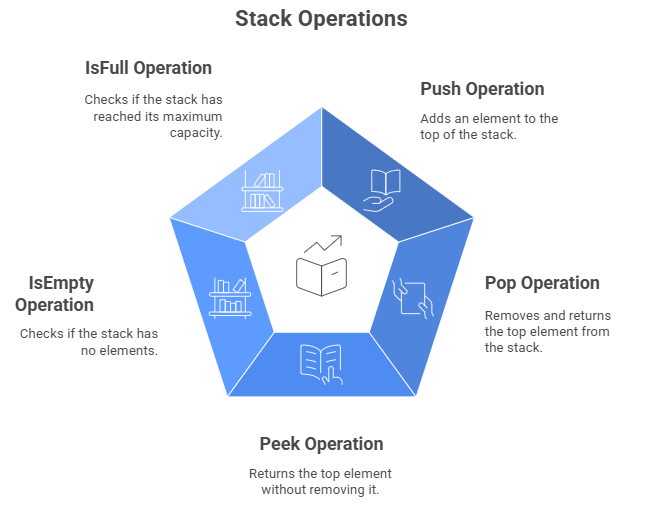
- push(): Adds an element to the top.
- pop(): Removes the top element.
- peek() or top(): Returns the top element without removing it.
- isEmpty(): Checks if the stack is empty.
- isFull() (if size is limited): Checks if the stack is full.
The time complexity of all the given operations is constant, i.e. O(1).
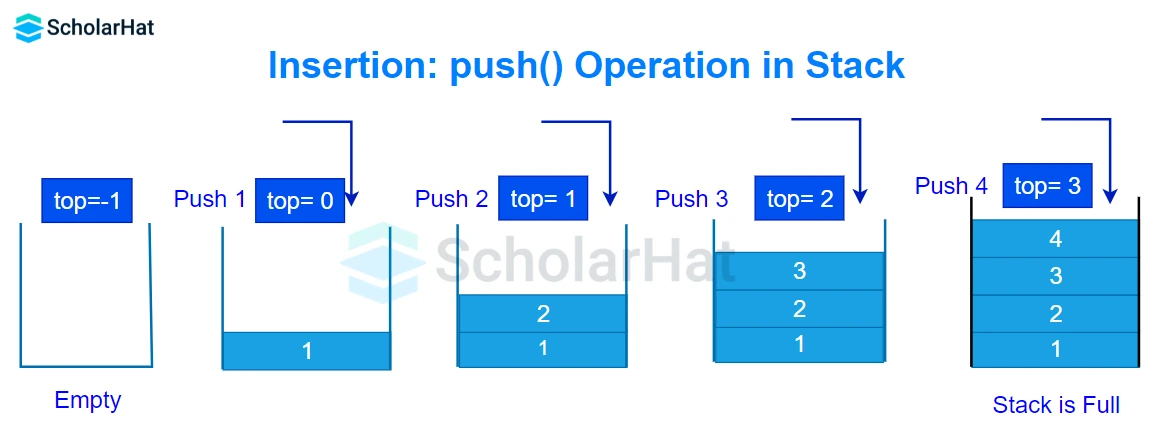
- Insertion: push()
The push() operation is one of the fundamental operations in a stack data structure. Pushing means inserting an element at the top of the stack. If the stack is full, then it is said to be an Overflow condition.
Algorithm for push() operation in the stack
begin
if stack is full
return
endif
else
increment top
stack[top] assign value
end else
end procedure
According to the algorithm,
- First Check if the stack is full
- If it is full, produce an error and exit
- If the stack is not full, increment top to point to the next space.
- Add the data element to the stack location, where the top is pointing.
- End the process and exit.
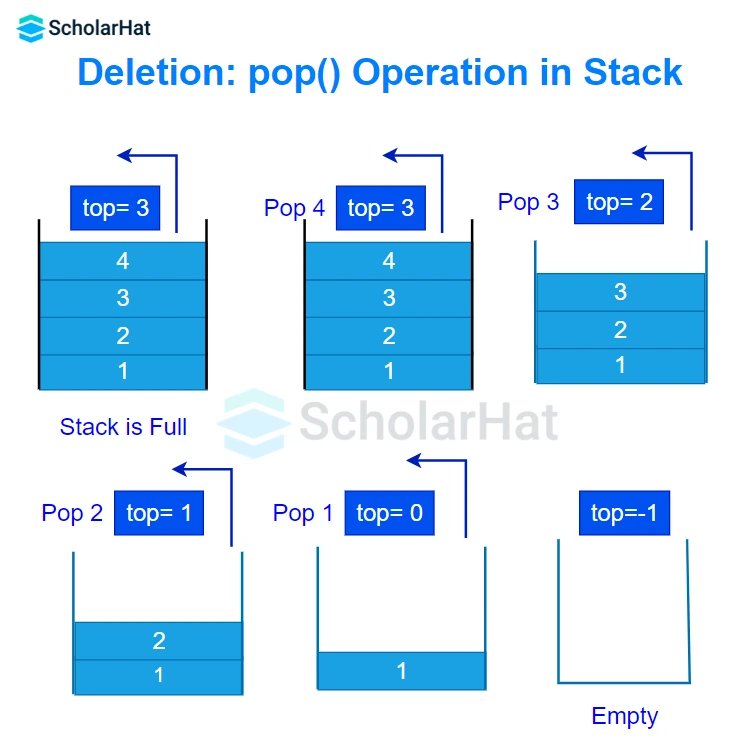
- Deletion: pop()
The pop() operation is used to remove the topmost element of the stack and return its value. The pop() operation modifies the state of the stack by removing the topmost element. The items are popped in the reversed order in which they are pushed. If the Stack is empty, it is a Underflow condition.
Algorithm for pop() operation on the stack
begin
if stack is empty
return
endif
else
store value of stack[top]
decrement top
return value
end else
end procedure
According to the algorithm,
- First, check if the stack is empty.
- If empty, print
Stack underflowand exit. - If not empty, access the data element at which the top is pointing.
- Decrease the value of the top by 1.
- End the process and exit.
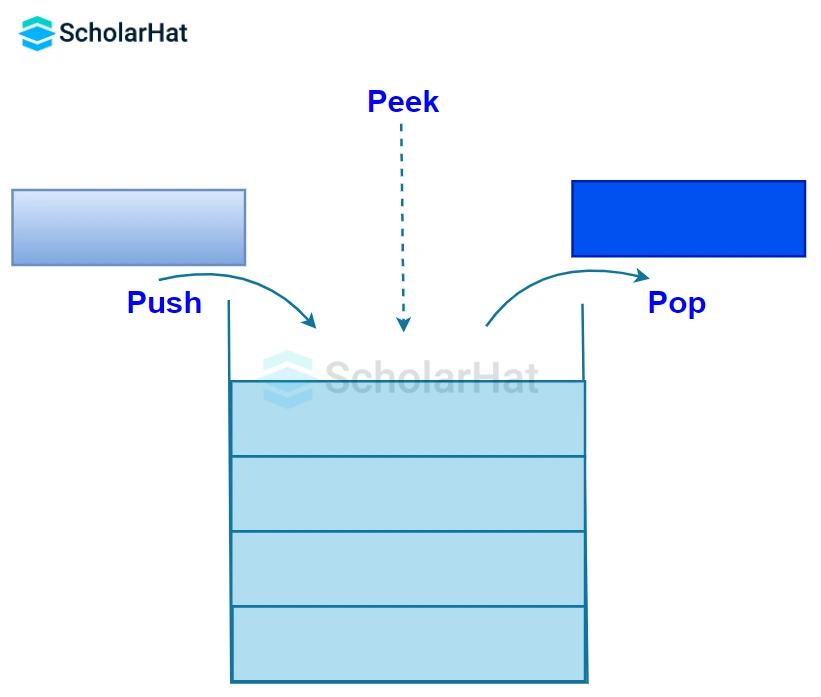
- peek()
The peek() operation returns the value of the topmost element of the stack without modifying the stack. This can be useful when you need to check the value of the top element before deciding whether to remove it or not.
Algorithm for peek() operation on the stack
begin
return stack[top]
end procedure
- isFull()
The isFull() operation is used to determine if the stack is full or not. A stack is said to be full if it has reached its maximum capacity and there is no more space to add new elements to the stack.
Algorithm for isFull() operation on the stack
begin
if stack length is equal to the maximum stack size
return true
endif
else
return false
end else
end procedure
- isEmpty()
The isEmpty() operation is used to check if the stack is empty or not. It returns a boolean value, true when the stack is empty, otherwise false.
Algorithm for isEmpty() operation on the stack
begin
if top < 1
return true
else
return false
end procedure
Working of Stack in Data Structures
The size of the stack depends on the number of memory blocks available to store the elements.
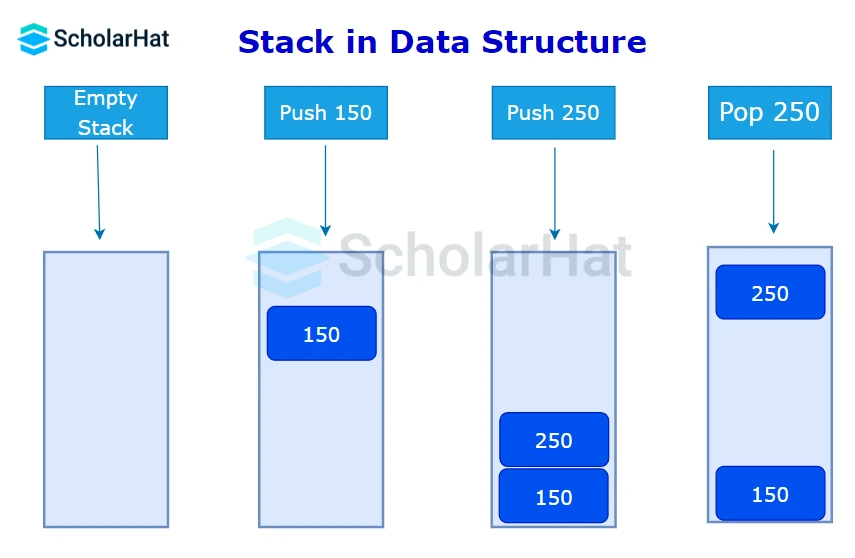
- Initially, as shown in the figure, the stack is empty, and we can add elements one by one using the push operation until it becomes full.
- A pointer called
TOPis used to keep track of the top element in the stack. - When initializing the stack, we set its value to -1 so that we can check if the stack is empty by comparing
TOP == -1. - On pushing an element, 150, we increase the value of TOP and place the new element in the position pointed to by TOP i.e.
TOP=0and sostack[0]=150. - Again we push n element, 250, and increase the value of TOP i.e.
TOP=1and sostack[1]=250. - On popping an element, we return the element pointed to by
TOPi.e.return stack[1]and reduce its value i.e.TOP=0. - Before pushing, we check if the stack is already full.
- Before popping, we check if the stack is already empty
Implementation of Stack in Different Programming Languages
There are two ways to implementStack in Data Structures, using a 1D Array and using a Single Linked List. Let us look at each of them.
The time complexity of all the operations in both implementations is the same i.e. O(1).
- Implementation of Stack Using a 1D Array
Follow the below-given procedure to implement stack using a 1D Array in Data Structures
- Declare a variable
topto keep track of the top element in the stack. - When initializing the stack, set the value of the
topto-1Check if the stack is full or empty. - Declare a function
push()that takes an array,stack[]; the size of the array,n; and element a is to be inserted as its parameters. - Under the function: you have to check if the stack is already full. If so, return from the function. and If the stack is not full, increment
topand place the new element in the position pointed to by thetop.
- Declare a function
pop()that removes thetopelement from the stack. - Under the function just check if the stack is empty. If so, return from the function then If the stack is not empty, return the element at the
topindex in the arraystack[]and decrementtop.Here, we are not deleting the value at the top index duringpop()because once the pointer is moved to point to the previous element, it does not matter what is contained in that memory location.
- Declare a function
topElement()that returns the element at thetopindex from the arraystack[]. - Declare a function
size()that returns the occupied size of the arraystack[]. It returnstop + 1. - Declare a function
isEmpty()to check if thetopis equal to-1. If it is, it returnstrue, otherwisefalse. - Declare a function
isFull()to check if thetopis equal to the maximum size of the arraystack[]. If it is, it returnstrue, otherwisefalse.
Example of Stack Implementation in Different Languages using a 1D array
#include <iostream>
using namespace std;
class Stack {
private:
int size;
int* stack;
int top;
public:
Stack(int size) {
this->size = size;
stack = new int[size];
top = -1;
}
void push(int a) {
if (top == size - 1) {
cout << "Stack Overflow" << endl;
} else {
stack[++top] = a;
}
}
bool isEmpty() {
return top == -1;
}
void pop() {
if (isEmpty()) {
cout << "Stack Underflow" << endl;
} else {
top--;
}
}
int stackSize() {
return top + 1;
}
int topElement() {
return stack[top];
}
~Stack() {
delete[] stack;
}
};
int main() {
Stack stack(6);
stack.push(5);
cout << "Current size of stack is " << stack.stackSize() << endl;
stack.push(10);
stack.push(15);
stack.push(20);
stack.push(25);
stack.push(30);
cout << "Current size of stack is " << stack.stackSize() << endl;
stack.push(35);
cout << "At present, the top element in stack is " << stack.topElement() << endl;
for (int i = 0; i < 6; ++i) {
stack.pop();
}
cout << "Current size of stack is " << stack.stackSize() << endl;
stack.pop();
return 0;
}
using System;
class Stack {
private int[] stack;
private int top;
private int size;
public Stack(int size) {
this.size = size;
stack = new int[size];
top = -1;
}
public void Push(int a) {
if (top == size - 1) {
Console.WriteLine("Stack Overflow");
} else {
stack[++top] = a;
}
}
public bool IsEmpty() {
return top == -1;
}
public void Pop() {
if (IsEmpty()) {
Console.WriteLine("Stack Underflow");
} else {
top--;
}
}
public int StackSize() {
return top + 1;
}
public int TopElement() {
return stack[top];
}
}
class Program {
static void Main() {
Stack stack = new Stack(6);
stack.Push(5);
Console.WriteLine("Current size of stack is " + stack.StackSize());
stack.Push(10);
stack.Push(15);
stack.Push(20);
stack.Push(25);
stack.Push(30);
Console.WriteLine("Current size of stack is " + stack.StackSize());
stack.Push(35);
Console.WriteLine("At present, the top element in stack is " + stack.TopElement());
for (int i = 0; i < 6; i++) {
stack.Pop();
}
Console.WriteLine("Current size of stack is " + stack.StackSize());
stack.Pop();
}
}
class Stack:
def __init__(self, size):
self.size = size
self.stack = [-1] * size
self.top = -1
def push(self, a):
if self.top == self.size - 1:
print("Stack Overflow")
else:
self.top += 1
self.stack[self.top] = a
def is_empty(self):
return self.top == -1
def pop(self):
if self.is_empty():
print("Stack Underflow")
else:
self.top -= 1
def stack_size(self):
return self.top + 1
def top_element(self):
return self.stack[self.top]
if __name__ == "__main__":
stack = Stack(6)
stack.push(5)
print("Current size of stack is", stack.stack_size())
stack.push(10)
stack.push(15)
stack.push(20)
stack.push(25)
stack.push(30)
print("Current size of stack is", stack.stack_size())
stack.push(35)
print("At present, the top element in stack is", stack.top_element())
for _ in range(6):
stack.pop()
print("Current size of stack is", stack.stack_size())
stack.pop()
class Stack {
private int size;
private int[] stack;
private int top;
public Stack(int size) {
this.size = size;
this.stack = new int[size];
this.top = -1;
}
public void push(int a) {
if (top == size - 1) {
System.out.println("Stack Overflow");
} else {
stack[++top] = a;
}
}
public boolean isEmpty() {
return top == -1;
}
public void pop() {
if (isEmpty()) {
System.out.println("Stack Underflow");
} else {
top--;
}
}
public int stackSize() {
return top + 1;
}
public int topElement() {
return stack[top];
}
}
public class Main {
public static void main(String[] args) {
Stack stack = new Stack(6);
stack.push(5);
System.out.println("Current size of stack is " + stack.stackSize());
stack.push(10);
stack.push(15);
stack.push(20);
stack.push(25);
stack.push(30);
System.out.println("Current size of stack is " + stack.stackSize());
stack.push(35);
System.out.println("At present, the top element in stack is " + stack.topElement());
for (int i = 0; i < 6; i++) {
stack.pop();
}
System.out.println("Current size of stack is " + stack.stackSize());
stack.pop();
}
}
class Stack {
private stack: number[];
private top: number;
private size: number;
constructor(size: number) {
this.size = size;
this.stack = new Array(size).fill(-1);
this.top = -1;
}
push(a: number): void {
if (this.top === this.size - 1) {
console.log("Stack Overflow");
} else {
this.top++;
this.stack[this.top] = a;
}
}
isEmpty(): boolean {
return this.top === -1;
}
pop(): void {
if (this.isEmpty()) {
console.log("Stack Underflow");
} else {
this.top--;
}
}
stackSize(): number {
return this.top + 1;
}
topElement(): number {
return this.stack[this.top];
}
}
const stack = new Stack(6);
stack.push(5);
console.log("Current size of stack is", stack.stackSize());
stack.push(10);
stack.push(15);
stack.push(20);
stack.push(25);
stack.push(30);
console.log("Current size of stack is", stack.stackSize());
stack.push(35);
console.log("At present, the top element in stack is", stack.topElement());
for (let i = 0; i < 6; i++) {
stack.pop();
}
console.log("Current size of stack is", stack.stackSize());
stack.pop();
Output
Current size of stack is 1
Current size of stack is 6
Stack Overflow
At present, the top element in stack is 30
Current size of stack is 0
Stack Underflow
Advantages of Array Implementation
- Easy to implement.
- Memory is saved as pointers are not involved.
Limitations of Array Implementation
- The maximum size of the array must be defined beforehand.
- The size of the array cannot be changed during the run time because it is not dynamic.
- Implementation of Stack Using a Single Linked List
Follow the below-given procedure to implement Stack using a Single Linked List in Data Structures.
- First of all, create a class or structure
Nodewith instance variables,data, andnext. - The
datawill contain the element to be inserted andnextwill contain the address of the previous element in the linked list. - To keep track of the topmost element, create an instance,
topof the classNode. - Declare a function
push()that takesdataas a parameter and adds it to the existing linked list. - Under the function –
- A temporary instance of the class
Nodeis created, and memory is allocated for the same. - Check if the heap is full. If it is, print
Stack Overflow. - If the heap is not full, add the data to the temporary instance.
- A temporary instance of the class
- Store the address of the previous
topin the address part of the temporary instance. - Update the
topso that it points to the temporary instance that contains the newly inserted value. - Declare a function
pop()that deletes the currenttop, and point it to the element just before it. - Under the function –
- Check if the stack is empty or not. If it is, print
Stack Underflow. - If the stack is not empty, make the
toppoint to the previous element. - Free the memory that was used by the element that was popped.
- Check if the stack is empty or not. If it is, print
Example of Stack Implementation in Different Languages Using a Single Linked List
#include <iostream>
class Node {
public:
int data;
Node* link;
Node(int value) {
data = value;
link = nullptr;
}
};
class Stack {
private:
Node* top;
public:
Stack() {
top = nullptr;
}
void push(int data) {
Node* temp = new Node(data);
temp->link = top;
top = temp;
}
bool isEmpty() {
return top == nullptr;
}
int peek() {
if (!isEmpty()) {
return top->data;
}
throw std::runtime_error("Stack is empty");
}
void pop() {
if (isEmpty()) {
std::cerr << "Stack Underflow" << std::endl;
exit(1);
}
Node* temp = top;
top = top->link;
delete temp;
}
};
int main() {
Stack stack;
stack.push(5);
stack.push(10);
stack.push(15);
stack.push(20);
stack.push(25);
stack.push(30);
std::cout << "The Top element is " << stack.peek() << std::endl;
stack.pop();
stack.pop();
stack.pop();
stack.pop();
stack.pop();
std::cout << "The Top element is " << stack.peek() << std::endl;
return 0;
}
using System;
class Node {
public int Data;
public Node Link;
public Node(int value) {
Data = value;
Link = null;
}
}
class Stack {
private Node top;
public Stack() {
top = null;
}
public void Push(int data) {
Node temp = new Node(data) {
Link = top
};
top = temp;
}
public bool IsEmpty() {
return top == null;
}
public int Peek() {
if (!IsEmpty()) {
return top.Data;
}
throw new InvalidOperationException("Stack is empty");
}
public void Pop() {
if (IsEmpty()) {
Console.WriteLine("Stack Underflow");
Environment.Exit(1);
}
top = top.Link;
}
}
class Program {
static void Main(string[] args) {
Stack stack = new Stack();
stack.Push(5);
stack.Push(10);
stack.Push(15);
stack.Push(20);
stack.Push(25);
stack.Push(30);
Console.WriteLine("The Top element is " + stack.Peek());
stack.Pop();
stack.Pop();
stack.Pop();
stack.Pop();
stack.Pop();
Console.WriteLine("The Top element is " + stack.Peek());
}
}
class Node:
def __init__(self, data):
self.data = data
self.link = None
class Stack:
def __init__(self):
self.top = None
def push(self, data):
temp = Node(data)
temp.link = self.top
self.top = temp
def is_empty(self):
return self.top is None
def peek(self):
if not self.is_empty():
return self.top.data
raise Exception("Stack is empty")
def pop(self):
if self.is_empty():
print("Stack Underflow")
exit(1)
self.top = self.top.link
if __name__ == "__main__":
stack = Stack()
stack.push(5)
stack.push(10)
stack.push(15)
stack.push(20)
stack.push(25)
stack.push(30)
print("The Top element is", stack.peek())
stack.pop()
stack.pop()
stack.pop()
stack.pop()
stack.pop()
print("The Top element is", stack.peek())
class Node {
int data;
Node link;
Node(int value) {
data = value;
link = null;
}
}
class Stack {
private Node top;
Stack() {
top = null;
}
void push(int data) {
Node temp = new Node(data);
temp.link = top;
top = temp;
}
boolean isEmpty() {
return top == null;
}
int peek() {
if (!isEmpty()) {
return top.data;
}
throw new RuntimeException("Stack is empty");
}
void pop() {
if (isEmpty()) {
System.err.println("Stack Underflow");
System.exit(1);
}
top = top.link;
}
}
public class Main {
public static void main(String[] args) {
Stack stack = new Stack();
stack.push(5);
stack.push(10);
stack.push(15);
stack.push(20);
stack.push(25);
stack.push(30);
System.out.println("The Top element is " + stack.peek());
stack.pop();
stack.pop();
stack.pop();
stack.pop();
stack.pop();
System.out.println("The Top element is " + stack.peek());
}
}
class Node {
data: number;
link: Node | null;
constructor(data: number) {
this.data = data;
this.link = null;
}
}
class Stack {
private top: Node | null;
constructor() {
this.top = null;
}
push(data: number): void {
const temp = new Node(data);
temp.link = this.top;
this.top = temp;
}
isEmpty(): boolean {
return this.top === null;
}
peek(): number {
if (!this.isEmpty()) {
return this.top!.data;
}
throw new Error("Stack is empty");
}
pop(): void {
if (this.isEmpty()) {
console.error("Stack Underflow");
process.exit(1);
}
this.top = this.top!.link;
}
}
const stack = new Stack();
stack.push(5);
stack.push(10);
stack.push(15);
stack.push(20);
stack.push(25);
stack.push(30);
console.log("The Top element is", stack.peek());
stack.pop();
stack.pop();
stack.pop();
stack.pop();
stack.pop();
console.log("The Top element is", stack.peek());
Output
Top element is: 30
Top element is: 5
If you are facing any difficulty in understanding the linked list implementation of stack in data structures refer to the previous tutorial, Linked Lists in Data Structures.
Advantages of Linked List Implementation
- A linked list is dynamic, i.e. the size of the linked list can be changed during the run time.
- It is used in many virtual machines like JVM.
Limitations of Linked List Implementation
- There's an extra memory requirement due to the involvement of pointers.
- Random accessing of elements is not possible in a stack.
Problems On Stack
1. Implement Stack using Array
Problem: Write a program to implement a stack using a fixed-size array
#include <iostream>
using namespace std;
class Stack {
private:
int* stack;
int top;
int size;
public:
Stack(int s) {
size = s;
stack = new int[size];
top = -1;
}
void push(int value) {
if (top == size - 1) {
cout << "Stack Overflow" << endl;
} else {
stack[++top] = value;
}
}
void pop() {
if (top == -1) {
cout << "Stack Underflow" << endl;
} else {
top--;
}
}
void display() {
if (top == -1) {
cout << "Stack is empty" << endl;
} else {
cout << "Stack elements: ";
for (int i = 0; i <= top; i++) {
cout << stack[i] << " ";
}
cout << endl;
}
}
~Stack() {
delete[] stack;
}
};
int main() {
Stack s(5);
s.push(10);
s.push(30);
s.display();
s.pop();
s.display();
return 0;
}
using System;
class Stack {
private int[] stack;
private int top;
private int size;
public Stack(int s) {
size = s;
stack = new int[size];
top = -1;
}
public void Push(int value) {
if (top == size - 1) {
Console.WriteLine("Stack Overflow");
} else {
stack[++top] = value;
}
}
public void Pop() {
if (top == -1) {
Console.WriteLine("Stack Underflow");
} else {
top--;
}
}
public void Display() {
if (top == -1) {
Console.WriteLine("Stack is empty");
} else {
Console.Write("Stack elements: ");
for (int i = 0; i <= top; i++) {
Console.Write(stack[i] + " ");
}
Console.WriteLine();
}
}
}
class Program {
static void Main(string[] args) {
Stack s = new Stack(5);
s.Push(10);
s.Push(30);
s.Display();
s.Pop();
s.Display();
}
}
class Stack:
def __init__(self, size):
self.size = size
self.stack = []
def push(self, value):
if len(self.stack) == self.size:
print("Stack Overflow")
else:
self.stack.append(value)
def pop(self):
if not self.stack:
print("Stack Underflow")
else:
self.stack.pop()
def display(self):
if not self.stack:
print("Stack is empty")
else:
print("Stack elements:", " ".join(map(str, self.stack)))
# Usage
s = Stack(5)
s.push(10)
s.push(30)
s.display()
s.pop()
s.display()
class Stack {
private int[] stack;
private int top;
private int size;
public Stack(int size) {
this.size = size;
stack = new int[size];
top = -1;
}
public void push(int value) {
if (top == size - 1) {
System.out.println("Stack Overflow");
} else {
stack[++top] = value;
}
}
public void pop() {
if (top == -1) {
System.out.println("Stack Underflow");
} else {
top--;
}
}
public void display() {
if (top == -1) {
System.out.println("Stack is empty");
} else {
System.out.print("Stack elements: ");
for (int i = 0; i <= top; i++) {
System.out.print(stack[i] + " ");
}
System.out.println();
}
}
}
public class Main {
public static void main(String[] args) {
Stack s = new Stack(5);
s.push(10);
s.push(30);
s.display();
s.pop();
s.display();
}
}
class Stack {
private stack: number[];
private top: number;
private size: number;
constructor(size: number) {
this.size = size;
this.stack = [];
this.top = -1;
}
push(value: number): void {
if (this.stack.length === this.size) {
console.log("Stack Overflow");
} else {
this.stack.push(value);
this.top++;
}
}
pop(): void {
if (this.top === -1) {
console.log("Stack Underflow");
} else {
this.stack.pop();
this.top--;
}
}
display(): void {
if (this.top === -1) {
console.log("Stack is empty");
} else {
console.log("Stack elements:", this.stack.join(" "));
}
}
}
// Usage
const s = new Stack(5);
s.push(10);
s.push(30);
s.display();
s.pop();
s.display();
Output
Stack elements: 10 20
Stack elements: 10
2. Check for Balanced Parentheses
Problem: Write a program to check if the given string of parentheses is balanced.
#include <iostream>
#include <stack>
bool isBalanced(const std::string &expression) {
std::stack<char> stack;
for (char ch : expression) {
if (ch == '(' || ch == '{' || ch == '[') {
stack.push(ch);
} else if (ch == ')' || ch == '}' || ch == ']') {
if (stack.empty()) return false;
char top = stack.top();
stack.pop();
if ((ch == ')' && top != '(') ||
(ch == '}' && top != '{') ||
(ch == ']' && top != '[')) {
return false;
}
}
}
return stack.empty();
}
int main() {
std::cout << isBalanced("({[]})") << std::endl; // 1
std::cout << isBalanced("([)]") << std::endl; // 0
return 0;
}
using System;
using System.Collections.Generic;
class Program {
static bool IsBalanced(string expression) {
Stack stack = new Stack();
foreach (char ch in expression) {
if (ch == '(' || ch == '{' || ch == '[') {
stack.Push(ch);
} else if (ch == ')' || ch == '}' || ch == ']') {
if (stack.Count == 0) return false;
char top = stack.Pop();
if ((ch == ')' && top != '(') ||
(ch == '}' && top != '{') ||
(ch == ']' && top != '[')) {
return false;
}
}
}
return stack.Count == 0;
}
static void Main() {
Console.WriteLine(IsBalanced("({[]})")); // True
Console.WriteLine(IsBalanced("([)]")); // False
}
}
def is_balanced(expression):
stack = []
for char in expression:
if char in "({[":
stack.append(char)
elif char in ")}]":
if not stack:
return False
top = stack.pop()
if char == ")" and top != "(":
return False
if char == "]" and top != "[":
return False
if char == "}" and top != "{":
return False
return not stack
print(is_balanced("({[]})")) # True
print(is_balanced("([)]")) # False
import java.util.Stack;
public class BalancedParentheses {
public static boolean isBalanced(String expression) {
Stack<Character> stack = new Stack<>();
for (char ch : expression.toCharArray()) {
if (ch == '(' || ch == '{' || ch == '[') {
stack.push(ch);
} else if (ch == ')' || ch == '}' || ch == ']') {
if (stack.isEmpty()) return false;
char top = stack.pop();
if ((ch == ')' && top != '(') ||
(ch == '}' && top != '{') ||
(ch == ']' && top != '[')) {
return false;
}
}
}
return stack.isEmpty();
}
public static void main(String[] args) {
System.out.println(isBalanced("({[]})")); // true
System.out.println(isBalanced("([)]")); // false
}
}
function isBalanced(expression: string): boolean {
const stack: string[] = [];
for (const char of expression) {
if (char === '(' || char === '{' || char === '[') {
stack.push(char);
} else if (char === ')' || char === '}' || char === ']') {
if (stack.length === 0) return false;
const top = stack.pop();
if ((char === ')' && top !== '(') ||
(char === '}' && top !== '{') ||
(char === ']' && top !== '[')) {
return false;
}
}
}
return stack.length === 0;
}
console.log(isBalanced("({[]})")); // true
console.log(isBalanced("([)]")); // false
Output
true
false3. Next Greater Element
Problem: Given an array, find the next greater element for each element using a stack.
#include <iostream>
#include <vector>
#include <stack>
using namespace std;
vector nextGreaterElement(vector& arr) {
vector result(arr.size(), -1);
stack s;
for (int i = 0; i < arr.size(); i++) {
while (!s.empty() && arr[s.top()] < arr[i]) {
result[s.top()] = arr[i];
s.pop();
}
s.push(i);
}
return result;
}
int main() {
vector arr1 = {4, 5, 2, 25};
vector arr2 = {13, 7, 6, 12};
vector result1 = nextGreaterElement(arr1);
vector result2 = nextGreaterElement(arr2);
for (int r : result1) cout << r << " ";
cout << endl;
for (int r : result2) cout << r << " ";
cout << endl;
return 0;
}
using System;
using System.Collections.Generic; // For Stack<int>
class Program {
static int[] NextGreaterElement(int[] arr) {
int[] result = new int[arr.Length];
Array.Fill(result, -1);
Stack<int> stack = new Stack<int>();
for (int i = 0; i < arr.Length; i++) {
while (stack.Count > 0 && arr[stack.Peek()] < arr[i]) {
int idx = stack.Pop();
result[idx] = arr[i];
}
stack.Push(i);
}
return result;
}
static void Main() {
int[] arr1 = { 4, 5, 2, 25 };
int[] arr2 = { 13, 7, 6, 12 };
Console.WriteLine(string.Join(" ", NextGreaterElement(arr1))); // Output: 5 25 25 -1
Console.WriteLine(string.Join(" ", NextGreaterElement(arr2))); // Output: -1 12 12 -1
}
}
def next_greater_element(arr):
stack = []
result = [-1] * len(arr)
for i in range(len(arr)):
while stack and arr[stack[-1]] < arr[i]:
idx = stack.pop()
result[idx] = arr[i]
stack.append(i)
return result
print(next_greater_element([4, 5, 2, 25])) # [5, 25, 25, -1]
print(next_greater_element([13, 7, 6, 12])) # [-1, 12, 12, -1]
import java.util.Stack;
public class NextGreaterElement {
public static int[] nextGreaterElement(int[] arr) {
int[] result = new int[arr.length];
Stack stack = new Stack<>();
for (int i = 0; i < arr.length; i++) {
result[i] = -1;
}
for (int i = 0; i < arr.length; i++) {
while (!stack.isEmpty() && arr[stack.peek()] < arr[i]) {
int idx = stack.pop();
result[idx] = arr[i];
}
stack.push(i);
}
return result;
}
public static void main(String[] args) {
int[] arr1 = {4, 5, 2, 25};
int[] arr2 = {13, 7, 6, 12};
for (int r : nextGreaterElement(arr1)) {
System.out.print(r + " ");
}
System.out.println();
for (int r : nextGreaterElement(arr2)) {
System.out.print(r + " ");
}
System.out.println();
}
}
function nextGreaterElement(arr: number[]): number[] {
const stack: number[] = [];
const result: number[] = new Array(arr.length).fill(-1);
for (let i = 0; i < arr.length; i++) {
while (stack.length > 0 && arr[stack[stack.length - 1]] < arr[i]) {
const idx = stack.pop()!;
result[idx] = arr[i];
}
stack.push(i);
}
return result;
}
console.log(nextGreaterElement([4, 5, 2, 25])); // [5, 25, 25, -1]
console.log(nextGreaterElement([13, 7, 6, 12])); // [-1, 12, 12, -1]
Output
5 25 25 -1
-1 12 12 -1
Applications of Stack
There are some applications of stacks in the data structure:
- Function Calls and Recursion: When a function is called, the compiler stores information about the return address and the values of any parameters, in the stack. When the function is finished, the information is retrieved from the stack and the program continues executing from the point where it left off.
- Recursion: To maintain the previous states, the compiler creates a system stack in which all the previous records of the function are maintained
- Expression Evaluation: A stack can be used to evaluate arithmetic expressions in which parentheses are used to group sub-expressions. The operands and operators are pushed into the stack, and when a closing parenthesis is encountered, the sub-expression is evaluated using the operators and operands in the stack.
- The A list of the expression conversion is given below:
- infix to prefix
- Infix to postfix
- Prefix to infix
- Prefix to postfix
- Postfix to infix
- Parsing: A stack is often used in parsing algorithms to keep track of the nesting of symbols such as parentheses, brackets, and braces.
- Undo/Redo Operations: Many applications, such as text editors and graphic design software, allow users to undo and redo previous operations. A stack can be used to store the state of the application before each operation, allowing the user to undo or redo the operation by popping or pushing elements from the stack.
- Backtracking: When searching for a solution to a problem, it may be necessary to backtrack and try a different path if the current path does not lead to a solution. A stack can be used to store information about the current path, allowing the algorithm to backtrack by popping elements from the stack.
Advantages of Stack
- Easy to implement: The implementation of a stack is simple, making it easy to use and understand.
- Efficient memory management: A stack uses a contiguous block of memory, which is allocated when the stack is created. This makes it efficient in terms of memory utilization.
- Accessibility: A stack allows quick access to its elements as the elements are added and removed from the top of the stack, which is useful in many applications, such as parsing expressions and reversing a string.
- Recursive algorithms:A stack is used to store function calls and their states, which helps in the efficient implementation of recursive function calls.
- Compiler Design: Stack is used in compiler design for parsing and syntax analysis of programming languages.
Disadvantages of Stack
- Limited storage: Stacks can store only a fixed number of elements. In the case of stack overflow, there can be a loss of data.
- No random access: Unlike other data structures like arrays, stacks do not provide direct access to elements in the middle of the stack. You can only add and remove elements from the top of the stack. The user has to remove all the elements above the middle element to access it.
- Stack overflow and underflow: Adding or removing too many elements into and from the stack can cause stack overflow or underflow respectively causing the program to crash.
- Memory management: Stack uses a contiguous block of memory, which can result in memory fragmentation or memory leaks if there's a frequent addition or removal of elements.
Conclusion
The stack is a simple yet powerful data structure that follows the Last In, First Out (LIFO) principle. It is widely used in programming for managing function calls, expressions, and undo operations. With its efficient operations and real-life applications, stack plays a crucial role in algorithm design. Understanding stack helps build a strong foundation in Data Structures and Algorithms (DSA).
With 18,000+ Java full stack jobs open in 2025, certified pros are in high demand. Secure your future with our Java full Stack Developer Course now!
FAQs
- There's an extra requirement of memory due to the involvement of pointers.
- Random accessing of elements is not possible in a stack.
Using an array as the underlying storage is one way to implement a stack. This approach is simple and fast, as both push and pop operations take constant time.
Take our Datastructures skill challenge to evaluate yourself!

In less than 5 minutes, with our skill challenge, you can identify your knowledge gaps and strengths in a given skill.