Prime Numbers in Java: Simple Logic and Code

Q: How can I check if a number is prime in Java

divTo check if a number is strongprimestrong you can iterate from strong2 strongto the strongsquare root of the numberstrong and check if any number divides it without a remainder If no divisors are found it’s strongprimestrongnbspdiv

Q: What is the most efficient way to check if a number is prime

divThe most efficient method is tostrong iteratestrong up to thestrong square root of the number strongand check divisibility Further optimizations can include skipping even numbers and known multiplesdivdivbrdiv

Q: How can I find all prime numbers in a given range in Java

divYou can loop through the range and use a prime-checking function for each number Then collect the numbers that pass the checknbspdiv

Q: What is the time complexity of prime number checking algorithms

divThe simple prime-checking algorithm has a time complexity ofstrong O√nstrong while the Sieve ofstrong Eratosthenesstrong has a time complexity of strongOn log log nstrongdivdivbrdiv

Q: Can I use BigInteger to check for large prime numbers in Java

divstrongYesstrong the strongBigInteger strongclass in Java has a method strongisProbablePrimeint certainty strongthat can check for primality for large numbersdivdivbrdiv

25 Sep 2024

Beginner

25 Views

60 min read

Prime Numbers in Java

Prime numbers in Java are those positive integer numbers that are greater than one(1) and do not have any positive divisors. You have learned about prime numbers and their mathematical operation in your academics. In Java, you have to find the prime numbers in programs by applying different types of algorithms.

In the Java tutorial, you will clear your thoughts about what are prime numbers in Java?, the importance of prime numbers in Java, prime vs. composite numbers, advanced topics in prime number theory, prime numbers in real-world applications, common pitfalls and best practices, and many more.

What are the Prime Numbers in Java?

Prime Numbers are those numbers which have greater value than one(1) divided by one(1) or itself only. In Java, you can use simple logic to check if a number is prime by testing its divisibility from 2 up to its square root. For example, 2, 3, 5, 7, 11, 13, 17, etc., are prime numbers. Now, You should also understand why prime numbers are important in programming.

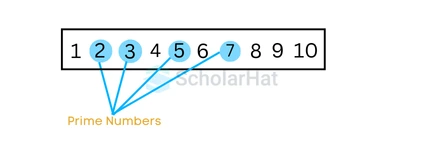
For an example, let's see the prime numbers between 1 to 10:

Importance of Prime Numbers in Programming

Prime numbers play an important role in programming. Let's understand this by some points that are following:

Cryptography: Used in encryption algorithms like RSA(Rivest–Shamir–Adleman) for secure communication.

Hash Functions: Prime numbers help reduce collisions in hash tables.

Random Number Generation: Primes ensure better distribution in random number sequences.

Algorithm Optimization: Used to solve problems in number theory and improve performance in mathematical computations.

Data Security: Prime factorization ensures robustness in securing sensitive information.

Must Read:

Java Full Stack Developer Roadmap for Beginners (Updated 2024)

Java Full Stack Developer Salary in India 2024 (Salary Guide)

Top 10 Reasons to Know Why Java is Important?

Mathematical Foundation of Prime Numbers

Prime numbers have a particular position in mathematics because of their distinct features. So, you should have patience and read carefully:

(A) Properties of Prime Numbers

There are several properties of prime numbers that are:

1. Divisibility Property

A prime number is divisible only by 1 and itself. It has exactly two distinct positive divisors: 1 and the prime number itself.
For example, 7 is a prime number because it can only be divided by 1 and 7 without leaving a remainder.

2. Uniqueness in Factorization (Fundamental Theorem of Arithmetic)

With the exception of factor order, every integer bigger than one may be uniquely factored as a product of prime integers.
30 may be factored, for instance, as 30=2×3×5, where 2, 3, and 5 are prime numbers.

3. Prime Density

As numbers increase, prime numbers become less frequent, though they are infinite. The distribution of primes becomes lesser as numbers grow larger.

4. Primes and Coprimes

The two different prime numbers are coprime (i.e., they have no common divisors other than 1) to each other.
For example, 5 and 11 are coprime.

5. Applications of Prime Numbers

Cryptography: Prime numbers are extensively used in public-key cryptography, particularly in the RSA algorithm, due to the difficulty of factoring large products of primes.
Number Theory: Primes are used to solve diophantine equations and understand the properties of integers.

(B) Prime vs. Composite Numbers

Here, you can understand the difference between prime and composite numbers in the following table:

Factors	Prime Numbers	Composite Numbers
Definition	Has only two distinct divisors: 1 and itself.	Has more than two distinct divisors.
Divisors	1 and the number itself.	1, itself, and at least one more divisor.
Smallest Example	2 (the only even prime).	4 (first composite number).
Example	2, 3, 5, 7, 11.	4, 6, 8, 9, 12.
Factorization	It cannot be factored into smaller numbers.	It can be factored into prime numbers.
Numbers of Deviors	Exactly two divisors.	More than two divisors.
Uniqueness	It cannot be expressed as a product of smaller numbers.	It can be expressed as a product of primes.

(C) Common Misconceptions about Prime Numbers

You should also get familiar with the common misconceptions about prime numbers that are:

1. "1 is a prime number"

Misunderstanding: Many believe that 1 is prime because it only has one divisor.
Fact: There must be precisely two different ways to divide a prime integer (1 and itself). One is not prime as it has just one divisor.

2. "All odd numbers are prime."

Misunderstanding: Many people believe that all odd numbers are prime.
Fact: Not all odd numbers are prime, even though all primes are odd (except from 2). Nine and fifteen, for instance, are unusual but not prime.

3. "Prime numbers get infinitely large without gaps."

Misunderstanding: Some assume that primes become more frequent as numbers grow larger.
Fact: As numbers rise, primes become less common, and the intervals between successive primes are wider.

4. "2 is an even number, so it's not prime."

Misunderstanding: Some believe no even number can be prime.
Fact: Because it has precisely two divisors, 2 is the only even prime number (1 and 2).

5. "A number divisible by a prime is also prime."

Misunderstanding: Some think if a number is divisible by a prime, it must also be prime.
Fact: If a number is divisible by a prime, it is composite, not prime. For instance, 10 is divisible by 2 and 5, both primes, but 10 itself is composite.

Read More:

Top 20 Java 8 Features to Boost Your Programming Skills

Differences between JDK, JRE, and JVM: Java Toolkit

Methods to Check for Prime Numbers in Java

You are familiar with the prime number concept. Now, let us move forward to learning methods to check prime numbers in Java:

1. Basic Method: Iterative Division

In Iterative division method, we check if a given number is divisible by any integer from 2 to n−1. If the number is divisible by any of these, it is not prime; otherwise, it is prime.

Example

public class PrimeCheck
{
    public static void main(String[] args)
    {
        int number = 29; // Example number to check
        if (isPrime(number))
        {
            System.out.println(number + " is a prime number.");
        }
        else
        {
            System.out.println(number + " is not a prime number.");
        }
    }

    // Function to check if a number is prime
    public static boolean isPrime(int n)
    {
        // Handle edge cases
        if (n <= 1)
        {
            return false; // 0, 1, and negative numbers are not prime
        }

        // Check for divisibility from 2 to n-1
        for (int i = 2; i < n; i++)
        {
            if (n % i == 0)
            {
                return false; // If divisible by any number, it's not prime
            }
        }
        return true; // If no divisors, the number is prime
    }
}

Output

29 is a prime number.

2. Improved Method: Square Root Optimization

The Square Root Optimization Method for checking if a number is prime in Java. This method significantly improves efficiency by checking divisibility only up to the square root of the number instead of checking all numbers up to n-1. If a number has a divisor larger than the square root of n, it will already have a corresponding smaller divisor.

Example

public class PrimeCheck {

    public static void main(String[] args) {
        int number = 29; // Example number to check
        if (isPrime(number)) {
            System.out.println(number + " is a prime number.");
        } else {
            System.out.println(number + " is not a prime number.");
        }
    }

    // Function to check if a number is prime using square root optimization
    public static boolean isPrime(int n) {
        // Handle edge cases
        if (n <= 1) return false; // 0, 1, and negative numbers are not prime
        if (n == 2) return true;  // 2 is the only even prime number
        if (n % 2 == 0) return false; // No other even number is prime

        // Only check divisibility from 3 to sqrt(n) and skip even numbers
        for (int i = 3; i * i <= n; i += 2) {
            if (n % i == 0) {
                return false; // If divisible by any number, it's not prime
            }
        }
        return true; // If no divisors are found, it's prime
    }
}

Output

29 is a prime number.

3. Advanced Method: Sieve of Eratosthenes

The Sieve of Eratosthenes is an efficient algorithm for finding all prime numbers up to a given limit n. It works by iteratively marking the multiples of each prime number starting from 2. The numbers which remain unmarked after processing are prime.

Example


import java.util.Arrays;

public class SieveOfEratosthenes {

    public static void main(String[] args) {
        int n = 50; // Find all primes up to 50
        sieveOfEratosthenes(n);
    }

    // Function to implement the Sieve of Eratosthenes algorithm
    public static void sieveOfEratosthenes(int n) {
        // Create a boolean array of size n+1, initially all set to true
        boolean[] isPrime = new boolean[n + 1];
        Arrays.fill(isPrime, true); // Assume all numbers are prime at first

        // Mark 0 and 1 as non-prime explicitly
        isPrime[0] = false;
        isPrime[1] = false;

        // Start from 2 and mark multiples of each number
        for (int i = 2; i * i <= n; i++) {
            // If i is still marked as prime, mark all its multiples as non-prime
            if (isPrime[i]) {
                for (int j = i * i; j <= n; j += i) {
                    isPrime[j] = false; // Mark multiples of i as non-prime
                }
            }
        }

        // Print all prime numbers
        System.out.println("Prime numbers up to " + n + ":");
        for (int i = 2; i <= n; i++) {
            if (isPrime[i]) {
                System.out.print(i + " ");
            }
        }
    }
}

Output

Prime numbers up to 50:
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47

Implementing Prime Number Programs in Java

1. Simple Prime Check Program

A simple prime check program in Java that accepts user input and provides various outputs based on whether the number is prime or not. The code will print different messages for prime and non-prime numbers.

Example

import java.util.Scanner;

public class PrimeCheck {
    
    public static void main(String[] args) {
        // Create a scanner object for user input
        Scanner scanner = new Scanner(System.in);

        // Ask the user to input a number
        System.out.print("Enter a number to check if it's prime: ");
        int number = scanner.nextInt();

        // Call the prime checking method and print different output
        if (isPrime(number)) {
            System.out.println(number + " is a prime number! It has only two divisors: 1 and " + number + ".");
        } else {
            System.out.println(number + " is not a prime number. It has more than two divisors.");
        }

        // Close the scanner
        scanner.close();
    }

    // Function to check if a number is prime
    public static boolean isPrime(int n) {
        if (n <= 1) {
            return false; // 0, 1, and negative numbers are not prime
        }
        // Check for divisibility up to sqrt(n)
        for (int i = 2; i <= Math.sqrt(n); i++) {
            if (n % i == 0) {
                return false; // If divisible, it's not prime
            }
        }
        return true; // If no divisors, it's prime
    }
}

Output

Enter a number to check if it's prime:
42 is not a prime number. It has more than two divisors.

2. Prime Numbers in a Given Range

Let's understand with an example where you can find the prime number in a given range by the user.

import java.util.Scanner;

public class PrimeInRange {

    public static void main(String[] args) {
        // Create a Scanner object for user input
        Scanner scanner = new Scanner(System.in);

        // Ask the user for the range
        System.out.print("Enter the start of the range: ");
        int start = scanner.nextInt();

        System.out.print("Enter the end of the range: ");
        int end = scanner.nextInt();

        // Display the prime numbers in the given range
        System.out.println("Prime numbers between " + start + " and " + end + ":");
        for (int i = start; i <= end; i++) {
            if (isPrime(i)) {
                System.out.print(i + " ");
            }
        }

        // Close the scanner
        scanner.close();
    }

    // Function to check if a number is prime
    public static boolean isPrime(int n) {
        // Handle edge cases
        if (n <= 1) {
            return false; // Numbers <= 1 are not prime
        }

        // Check divisibility from 2 to sqrt(n)
        for (int i = 2; i * i <= n; i++) {
            if (n % i == 0) {
                return false; // If divisible by i, it's not prime
            }
        }

        return true; // If no divisors found, it's prime
    }
}

In this example, you can provide any range of numbers and find the prime numbers in Java. Suppose you have given 10 and 20 as the range of the numbers to find the prime numbers in Java.

Enter the start of the range: 10
Enter the end of the range: 20

Output

Prime numbers between 10 and 20:
11 13 17 19

3. Prime Number Program Using Recursion

You can also find the prime numbers in Java using the recursion method. This approach recursively checks for divisibility from 2 up to the square root of the number.

Example

import java.util.Scanner;

public class PrimeCheckRecursive {

    public static void main(String[] args) {
        // Create a Scanner object for user input
        Scanner scanner = new Scanner(System.in);

        // Ask the user to enter a number to check if it's prime
        System.out.print("Enter a number: ");
        int number = scanner.nextInt();

        // Check if the number is prime using a recursive method
        if (isPrime(number, 2)) {
            System.out.println(number + " is a prime number.");
        } else {
            System.out.println(number + " is not a prime number.");
        }

        // Close the scanner
        scanner.close();
    }

    // Recursive function to check if a number is prime
    public static boolean isPrime(int n, int i) {
        // Base case 1: If number is less than 2, it's not prime
        if (n <= 1) {
            return false;
        }
        // Base case 2: If i exceeds the square root of n, n is prime
        if (i * i > n) {
            return true;
        }
        // Check if n is divisible by i
        if (n % i == 0) {
            return false; // If divisible, n is not prime
        }
        // Recursive call with the next number
        return isPrime(n, i + 1);
    }
}

Output

Enter a number: 30
30 is not a prime number.

4. Displaying First N Prime Numbers

We have given you an example to help you understand how to print the first N prime numbers in Java. The program takes an input N from the user and then finds and prints the first N prime numbers in Java using a simple iterative approach.

Example

import java.util.Scanner;

public class FirstNPrimes {

    public static void main(String[] args) {
        // Create a Scanner object for user input
        Scanner scanner = new Scanner(System.in);

        // Ask the user for the number of prime numbers to display
        System.out.print("Enter the number of prime numbers you want to display: ");
        int n = scanner.nextInt();

        // Check for valid input
        if (n <= 0) {
            System.out.println("Please enter a positive integer.");
        } else {
            // Display the first N prime numbers
            System.out.println("The first " + n + " prime numbers are:");
            printFirstNPrimes(n);
        }

        // Close the scanner
        scanner.close();
    }

    // Function to print the first N prime numbers
    public static void printFirstNPrimes(int n) {
        int count = 0; // Count of prime numbers found
        int num = 2;   // Start checking from the first prime number

        // Loop until we've found the first N primes
        while (count < n) {
            if (isPrime(num)) {
                System.out.print(num + " ");
                count++; // Increment the count of primes found
            }
            num++; // Move to the next number
        }
    }

    // Function to check if a number is prime
    public static boolean isPrime(int n) {
        // Handle edge cases
        if (n <= 1) {
            return false; // Numbers <= 1 are not prime
        }

        // Check divisibility from 2 to sqrt(n)
        for (int i = 2; i * i <= n; i++) {
            if (n % i == 0) {
                return false; // If divisible by i, it's not prime
            }
        }

        return true; // If no divisors found, it's prime
    }
}

Output

Enter the number of prime numbers you want to display:4
The first 4 prime numbers are: 2 3 5 7

5. Prime Factorization Program

Let's understand by an example. The program takes an integer input from the user and prints its prime factors.

Example

import java.util.Scanner;

public class PrimeFactorization {

    public static void main(String[] args) {
        // Create a Scanner object for user input
        Scanner scanner = new Scanner(System.in);

        // Ask the user to enter a number to factorize
        System.out.print("Enter a number to find its prime factors: ");
        int number = scanner.nextInt();

        // Display the prime factors of the entered number
        System.out.print("Prime factors of " + number + " are: ");
        findPrimeFactors(number);

        // Close the scanner
        scanner.close();
    }

    // Function to find and print prime factors of a number
    public static void findPrimeFactors(int n) {
        // Handle negative input
        if (n < 0) {
            System.out.println("Please enter a positive integer.");
            return;
        }

        // Print the number of 2s that divide n
        while (n % 2 == 0) {
            System.out.print(2 + " ");
            n /= 2;
        }

        // n must be odd at this point, so we can skip even numbers
        for (int i = 3; i * i <= n; i += 2) {
            // While i divides n, print i and divide n
            while (n % i == 0) {
                System.out.print(i + " ");
                n /= i;
            }
        }

        // This condition is to handle the case when n is a prime number greater than 2
        if (n > 2) {
            System.out.print(n);
        }
    }
}

Output

Enter a number to find its prime factors: 72
Prime factors of 72 are: 2 2 2 3 3

Also Read:

Lambda Expressions in Java: Explained in Easy Steps

Typecasting in Java: A Detailed Explanation with Example

Fibonacci Series in Java using Recursion, Scanner, For & While Loop

Optimizing Prime Number Algorithms

Optimizing prime number algorithms is crucial for improving performance, especially when working with large numbers or generating many primes. Here are several strategies and advanced methods to optimize prime-checking and prime-generation algorithms in Java

1. Algorithmic Optimization

Square Root Optimization: Check divisibility only up to the square root of n, reducing checks significantly.

Skip Even Numbers After 2: Check only odd numbers, halving the operations.

Sieve of Eratosthenes: Efficiently generates all primes up to n using a marking technique.

Segmented Sieve: Extends the Sieve for large ranges without recalculating smaller primes.

Wheel Factorization: Skips multiples of small primes (e.g., 2, 3, 5) for faster prime checks.

Miller-Rabin Test: Probabilistic test for quickly verifying large prime numbers.

Wheel Factorization Example

public class WheelFactorization {

    public static void main(String[] args) {
        int number = 97;  // Example number to check
        if (isPrime(number)) {
            System.out.println(number + " is a prime number.");
        } else {
            System.out.println(number + " is not a prime number.");
        }
    } // End of main method

    // Function to check if a number is prime using wheel factorization
    public static boolean isPrime(int n) {
        if (n <= 1) 
            return false; // Numbers <= 1 are not prime

        if (n == 2 || n == 3 || n == 5) 
            return true; // 2, 3, and 5 are primes

        if (n % 2 == 0 || n % 3 == 0 || n % 5 == 0) 
            return false; // Eliminate multiples of 2, 3, and 5

        // Check divisibility using increments based on the wheel (skipping multiples of 2, 3, 5)
        int[] wheel = {4, 2, 4, 2, 4, 6, 2, 6}; // Pattern to skip unnecessary checks
        int i = 7; // Start checking from the first number after 5
        int wheelIndex = 0;

        while (i * i <= n) {
            if (n % i == 0) 
                return false; // If divisible, it's not prime
            
            i += wheel[wheelIndex]; // Move to the next index in the wheel pattern
            wheelIndex = (wheelIndex + 1) % wheel.length; // Cycle through the wheel pattern
        }

        return true; // If no divisors found, the number is prime
    } // End of isPrime function

} // End of WheelFactorization class

Output

97 is a prime number.

2. Memory Management Techniques

Here, you will learn two memory management techniques that are explained below

(a) Garbage Collection

What It Is: Think of it like cleaning up your room. When you have toys or things that you no longer use, you throw them away to make space.

How It Works: In programming, when you create objects (like toys) but later don’t need them anymore, garbage collection automatically finds these unused objects and removes them to free up memory.

Example

In Java, if you create a string like "Hello" but later set it to null (meaning you don’t need it anymore), the garbage collector will eventually clear that memory for you.

public class GarbageCollectionExample {
    public static void main(String[] args) {
        // Create an object
        String str = new String("Hello, World!");

        // Set the reference to null to make it eligible for garbage collection
        str = null;

        // Request garbage collection
        System.gc(); // This is just a request; it may not happen immediately
        System.out.println("Garbage collection requested.");
    }
}

Output

Garbage collection requested.

(b) Memory Pooling

What It Is: Imagine you have a toy box where you keep all your toys. Instead of buying new toys every time you want to play, you can just take one out of the box and put it back when you're done.

How It Works: In programming, a memory pool is like a toy box. You create a set of objects (toys) in advance and reuse them instead of creating new ones each time, which saves time and memory.

Example

If you’re making a game and need many bullets, you can create a pool of bullet objects. When a bullet is fired, you take one from the pool, and when it’s no longer needed, you put it back in the pool for reuse.

import java.util.ArrayList;
import java.util.List;

class ObjectPool {
    private List pool;

    public ObjectPool(int size) {
        pool = new ArrayList<>(size);
        // Adding some objects to the pool
        for (int i = 0; i < size; i++) {
            pool.add("Object " + i);
        }
    }

    public String acquire() {
        // Get an object from the pool
        if (pool.isEmpty()) {
            return null; // No objects available
        }
        return pool.remove(pool.size() - 1); // Take the last object
    }

    public void release(String obj) {
        // Put the object back into the pool
        pool.add(obj);
    }
}

public class MemoryPoolingExample {
    public static void main(String[] args) {
        ObjectPool objectPool = new ObjectPool(5); // Create a pool of 5 objects

        String obj1 = objectPool.acquire(); // Take an object from the pool
        System.out.println("Acquired: " + obj1);
        
        objectPool.release(obj1); // Put the object back in the pool
        System.out.println("Released: " + obj1);
    }
}

Output

Acquired: Object 4
Released: Object 4

3. Parallel Processing for Large Datasets

There are three important parallel processing techniques you will learn here, which are below.

(a) Fork/Join Framework

The Fork/Join framework is designed to take advantage of multiple processors by breaking down a large task into smaller subtasks, processing them in parallel, and then combining the results.

Example

import java.util.concurrent.RecursiveTask;
import java.util.concurrent.ForkJoinPool;

class PrimeTask extends RecursiveTask {
    private int start, end;

    public PrimeTask(int start, int end) {
        this.start = start;
        this.end = end;
    }

    @Override
    protected Integer compute() {
        if (end - start <= 1000) { // Base case for small ranges
            return countPrimesInRange(start, end);
        }
        int mid = (start + end) / 2;
        PrimeTask leftTask = new PrimeTask(start, mid);
        PrimeTask rightTask = new PrimeTask(mid, end);
        leftTask.fork(); // Asynchronously execute the left task
        return rightTask.compute() + leftTask.join(); // Combine results
    }

    private int countPrimesInRange(int start, int end) {
        int count = 0;
        for (int i = start; i < end; i++) {
            if (isPrime(i)) {
                count++;
            }
        }
        return count;
    }

    private boolean isPrime(int n) {
        if (n <= 1) return false;
        for (int i = 2; i * i <= n; i++) {
            if (n % i == 0) return false;
        }
        return true;
    }
}

public class ParallelPrime {
    public static void main(String[] args) {
        ForkJoinPool pool = new ForkJoinPool();
        int start = 1, end = 100000; // Range for prime checking
        PrimeTask task = new PrimeTask(start, end);
        int primeCount = pool.invoke(task);
        System.out.println("Total primes found: " + primeCount);
    }
}

Output

Total primes found: 9592

(b) ExecutorService

The ExecutorService framework allows you to manage a pool of threads and submit tasks for asynchronous execution. You can split the workload into multiple tasks and run them concurrently.

Example

import java.util.concurrent.ExecutorService;
import java.util.concurrent.Executors;
import java.util.concurrent.Future;

public class ExecutorServicePrime {
    public static void main(String[] args) throws Exception {
        int start = 1, end = 100000;
        int numThreads = 10; // Number of threads
        ExecutorService executor = Executors.newFixedThreadPool(numThreads);
        Future[] results = new Future[numThreads];
        int chunkSize = (end - start) / numThreads;

        // Submit tasks
        for (int i = 0; i < numThreads; i++) {
            final int chunkStart = start + i * chunkSize;
            final int chunkEnd = (i == numThreads - 1) ? end : chunkStart + chunkSize;
            results[i] = executor.submit(() -> countPrimesInRange(chunkStart, chunkEnd));
        }

        // Collect results
        int totalPrimes = 0;
        for (Future result : results) {
            totalPrimes += result.get(); // Get the result from each task
        }

        executor.shutdown(); // Shutdown the executor
        System.out.println("Total primes found: " + totalPrimes);
    }

    private static int countPrimesInRange(int start, int end) {
        int count = 0;
        for (int i = start; i < end; i++) {
            if (isPrime(i)) count++;
        }
        return count;
    }

    private static boolean isPrime(int n) {
        if (n <= 1) return false;
        for (int i = 2; i * i <= n; i++) {
            if (n % i == 0) return false;
        }
        return true;
    }
}

Output

Total primes found: 9592

(c) Parallel Streams (Java 8 and Above)

Java 8 introduced the Streams API, which allows you to process collections of data in a functional style. The parallelStream() method enables parallel processing of data.

Example

import java.util.stream.IntStream;

public class ParallelStreamsPrime {
    public static void main(String[] args) {
        int start = 1, end = 100000; // Range for prime checking
        long primeCount = IntStream.range(start, end)
                                    .parallel() // Enable parallel processing
                                    .filter(ParallelStreamsPrime::isPrime)
                                    .count(); // Count primes

        System.out.println("Total primes found: " + primeCount);
    }

    private static boolean isPrime(int n) {
        if (n <= 1) return false;
        return IntStream.rangeClosed(2, (int) Math.sqrt(n))
                        .noneMatch(i -> n % i == 0); // Check for factors
    }
}

Output

Total primes found: 9592

Prime Numbers in Real-world Applications

1. Prime Numbers in Cryptography

RSA Encryption: Relies on the product of two large prime numbers for secure key generation.

Diffie-Hellman Key Exchange: Uses prime numbers to facilitate secure shared key creation over an insecure channel.

Digital Signatures: Employs prime numbers in algorithms like DSA for authenticating messages.

Hash Functions: Some cryptographic hash functions use prime numbers to generate unique hash values.

Secure Communication Protocols: Protocols like SSL/TLS use prime numbers to establish secure connections.

2. Prime Number in Hashing

Hash Functions: Prime numbers are often used in hash functions to minimize collisions and evenly distribute hash values across the available range.

Modulus Operation: Using a prime number as the modulus in hash calculations helps ensure a more uniform distribution of hash codes.

Load Balancing: In data structures like hash tables, prime numbers can improve load balancing, reducing clustering and enhancing performance.

Hash Table Size: Choosing the size of a hash table as a prime number can reduce the likelihood of collision when multiple keys hash to the same index.

Efficient Operations: Prime numbers enable efficient operations in algorithms, as their unique properties can simplify calculations and enhance security in data handling.

3. Prime Numbers in Random Number Generation

Seed Selection: Primes can enhance the randomness of seed values in algorithms.

Algorithm Efficiency: Primality improves the efficiency of certain random number algorithms.

Cycle Length: Primes contribute to longer cycles in pseudorandom number generators.

Statistical Properties: Primes help achieve better statistical distribution in random sequences.

Advanced Topics in Prime Number Theory

1 Generating Large Prime Numbers

Purpose: Essential for cryptography, particularly in algorithms like RSA, where large primes secure data encryption.

Bit Length: Commonly 1024 to 4096 bits, depending on the security requirements.

Methods:
- Probabilistic Tests: Algorithms such as Miller-Rabin and Fermat tests are used to quickly identify probable primes.
- Sieve Algorithms: The Sieve of Eratosthenes is effective for finding smaller primes but less efficient for very large numbers.

Example

import java.math.BigInteger;
import java.security.SecureRandom;

public class LargePrimeGenerator {
    public static void main(String[] args) {
        SecureRandom random = new SecureRandom();
        BigInteger prime = BigInteger.probablePrime(2048, random);
        System.out.println("Generated Large Prime: " + prime);
    }
}

Output


Generated Large Prime: 29846303446733845060737949120506354686274238316388388490510993614489492335091320589650386327176436116794837961239521660933194040307474865486918024933039962968820772223204553760395540648351334966880495340824001292533560393866737953285889386149040602560646842232893277076242057054597142816285476531804525631411010972248378965180218934938700564170314937764166006075865412770850217273390144335039841826107164502247371074724385491562326763159735566672578199268675215442920545479391660257627537144230534103808200799075678888906520102641010039720952531569448835283272744011688335074378839616939184056298200094762129811835301

2. Probabilistic Prime Testing

Purpose: Quickly assess if a large number is prime.

Nature: Provides a high probability of primality, not absolute certainty.

Common Algorithms:
- Miller-Rabin Test: Tests multiple random bases; detects composites.
- Fermat's Little Theorem: Relies on modular arithmetic; can yield false positives.

3 Prime Number Theorems and Conjectures

Prime Number Theorem: Asserts that the number of primes less than n is approximately n/log(n), illustrating their distribution.

Riemann Hypothesis: A famous unsolved conjecture stating that all non-trivial zeros of the Riemann zeta function lie on the line Re(s)=1/2.

Goldbach's Conjecture: Proposes that every even integer greater than 2 can be expressed as the sum of two prime numbers.

Twin Prime Conjecture: Suggests that there are infinitely many pairs of primes (p,p+2) such that both numbers are prime.

Common Pitfalls and Best Practices

Common Pitfalls of Prime Numbers in Java

Inefficient Algorithms: Using basic trial division for large numbers can be slow; opt for optimized methods like the Sieve of Eratosthenes or probabilistic tests.

Incorrect Prime Checks: Failing to handle edge cases, such as negative numbers or zero, which are not prime.

Overlooking Performance: Ignoring the efficiency of algorithms when generating large prime numbers, leading to timeouts or slow performance in applications.

Assuming Randomness: Using random number generation without checking if the result is prime, which can lead to unexpected behavior.

Best Practices of Prime Numbers in Java

Use BigInteger: To handle very large prime numbers, utilize the BigInteger class for accurate computations and built-in primality tests.

Precompute Small Primes: Store a list of small prime numbers to speed up checks and computations involving larger numbers.

Implement Efficient Algorithms: Use advanced algorithms like the Sieve of Eratosthenes to generate a list of primes and probabilistic tests for primality checking.

Profile Performance: Regularly profile and test your prime number algorithms to ensure they perform well under expected conditions.

Must Read:

Top 50 Java MCQ Questions

Java Interview Questions for Freshers, 3, 5, and 10 Years Experience

Java Multithreading Interview Questions and Answers 2024

Top 50+ Java 8 Interview Questions & Answers 2024 [Updated]

Conclusion

In conclusion, we have covered the Prime numbers in Java. Prime numbers in Java are essential for many uses, particularly in cryptography, where they guarantee data integrity and safe transmission. Java offers strong tools and methods for working with prime numbers in an effective manner, such as the RSA encryption and the Miller-Rabin test. For a better understanding of Java programming, ScholarHat provides the Full-Stack Java Developer Certification Training Course, which will help you make a brighter career in Java application development.

FAQs

Q1. How can I check if a number is prime in Java?

To check if a number is prime, you can iterate from 2 to the square root of the number and check if any number divides it without a remainder. If no divisors are found, it’s prime.

Q2. What is the most efficient way to check if a number is prime?

The most efficient method is to iterate up to the square root of the number and check divisibility. Further optimizations can include skipping even numbers and known multiples.

Q3. How can I find all prime numbers in a given range in Java?

You can loop through the range and use a prime-checking function for each number. Then, collect the numbers that pass the check.

Q4. What is the time complexity of prime number checking algorithms?

The simple prime-checking algorithm has a time complexity of O(√n), while the Sieve of Eratosthenes has a time complexity of O(n log log n).

Q5. Can I use BigInteger to check for large prime numbers in Java?

Yes, the BigInteger class in Java has a method isProbablePrime(int certainty) that can check for primality for large numbers.

Advanced Full-Stack .NET Developer Certification Training	Oct 05	SAT, SUN	Filling Fast 08:30PM to 10:30PM (IST)	Get Details
ASP.NET Core Certification Training	Oct 05	SAT, SUN	Filling Fast 08:30PM to 10:30PM (IST)	Get Details
Angular Certification Training	Oct 06	SAT, SUN	Filling Fast 08:30PM to 10:30PM (IST)	Get Details
Full-Stack .NET Developer Certification Training	Oct 06	SAT, SUN	Filling Fast 07:00AM to 09:00AM (IST)	Get Details
ASP.NET Core Project	Oct 19	SAT, SUN	Filling Fast 10:00AM to 12:00PM (IST)	Get Details
.NET Solution Architect Certification Training	Oct 20	SAT, SUN	Filling Fast 05:30PM to 07:30PM (IST)	Get Details
.NET Microservices Certification Training	Oct 20	SAT, SUN	Filling Fast 05:30PM to 07:30PM (IST)	Get Details
Advanced Full-Stack .NET Developer Certification Training	Oct 20	SAT, SUN	Filling Fast 09:30AM to 11:30AM (IST)	Get Details
ASP.NET Core Certification Training	Oct 20	SAT, SUN	Filling Fast 09:30AM to 11:30AM (IST)	Get Details
Azure Developer Certification Training	Oct 27	SAT, SUN	Filling Fast 08:30PM to 10:30PM (IST)	Get Details

01 Career Opportunities

02 Beginner

03 Intermediate

04 Questions

05 Training Programs

Prime Numbers in Java: Simple Logic and Code

Java Online Course Free with Certificate (2024)

Prime Numbers in Java

What are the Prime Numbers in Java?

Importance of Prime Numbers in Programming

Mathematical Foundation of Prime Numbers

(A) Properties of Prime Numbers

1. Divisibility Property

2. Uniqueness in Factorization (Fundamental Theorem of Arithmetic)

3. Prime Density

4. Primes and Coprimes

5. Applications of Prime Numbers

(B) Prime vs. Composite Numbers

(C) Common Misconceptions about Prime Numbers

1. "1 is a prime number"

2. "All odd numbers are prime."

3. "Prime numbers get infinitely large without gaps."

4. "2 is an even number, so it's not prime."

5. "A number divisible by a prime is also prime."

Methods to Check for Prime Numbers in Java

1. Basic Method: Iterative Division

Example

Output

2. Improved Method: Square Root Optimization

Example

Output

3. Advanced Method: Sieve of Eratosthenes

Example

Output

Implementing Prime Number Programs in Java

1. Simple Prime Check Program

Example

Output

2. Prime Numbers in a Given Range

Output

3. Prime Number Program Using Recursion

Example

Output

4. Displaying First N Prime Numbers

Example

Output

5. Prime Factorization Program

Example

Output

Optimizing Prime Number Algorithms

1. Algorithmic Optimization

Wheel Factorization Example

Output

2. Memory Management Techniques

(a) Garbage Collection

Example

Output

(b) Memory Pooling

Example

Output

3. Parallel Processing for Large Datasets

(a) Fork/Join Framework

Example

Output

(b) ExecutorService

Example

Output

(c) Parallel Streams (Java 8 and Above)

Example

Output

Prime Numbers in Real-world Applications

1. Prime Numbers in Cryptography

2. Prime Number in Hashing

3. Prime Numbers in Random Number Generation

Advanced Topics in Prime Number Theory

1 Generating Large Prime Numbers

Example

Output

2. Probabilistic Prime Testing

3 Prime Number Theorems and Conjectures