Model Selection for Machine Learning

Introduction

Model selection is an essential phase in the development of powerful and precise predictive models in the field of machine learning. Model selection is the process of deciding which algorithm and model architecture is best suited for a particular task or dataset. It entails contrasting various models, assessing their efficacy, and choosing the one that most effectively addresses the issue at hand.

The choice of an appropriate machine learning model is crucial since there are various levels of complexity, underlying assumptions, and capabilities among them. A model's ability to generalize to new, untested data may not be as strong as its ability to perform effectively on a single dataset or problem. Finding a perfect balance between the complexity of models & generalization is therefore key to model selection.

Choosing a model often entails a number of processes. The first step in this process is to define a suitable evaluation metric that matches the objectives of the particular situation. According to the nature of the issue, this statistic may refer to precision, recall, accuracy, F1-score, or any other relevant measure.

The selection of numerous candidate models is then made in accordance with the problem at hand and the data that are accessible. These models might be as straightforward as decision trees or linear regression or as sophisticated as deep neural networks, random forests, or support vector machines. During the selection process, it is important to take into account the assumptions, constraints, and hyperparameters that are unique to each model.

Using a suitable methodology, such as cross-validation, the candidate models are trained and evaluated after being selected. To do this, the available data must be divided into validation and training sets, with each model fitting on the training set before being evaluated on the validation set. The models are compared using their performance metrics, then the model with the highest performance is chosen.

Model selection is a continuous process, though. In order to make wise selections, it frequently calls for an iterative process that involves testing several models and hyperparameters. The models are improved through this iterative process, which also aids in choosing the ideal mix of algorithms & hyperparameters.

Model Selection

In machine learning, the process of selecting the top model or algorithm from a list of potential models to address a certain issue is referred to as model selection. It entails assessing and contrasting various models according to how well they function and choosing the one that reaches the highest level of accuracy or prediction power.

Because different models have varied levels of complexity, underlying assumptions, and capabilities, model selection is a crucial stage in the machine-learning pipeline. Finding a model that fits the training set of data well and generalizes well to new data is the objective. While a model that is too complex may overfit the data and be unable to generalize, a model that is too simple could underfit the data and do poorly in terms of prediction.

The following steps are frequently included in the model selection process:

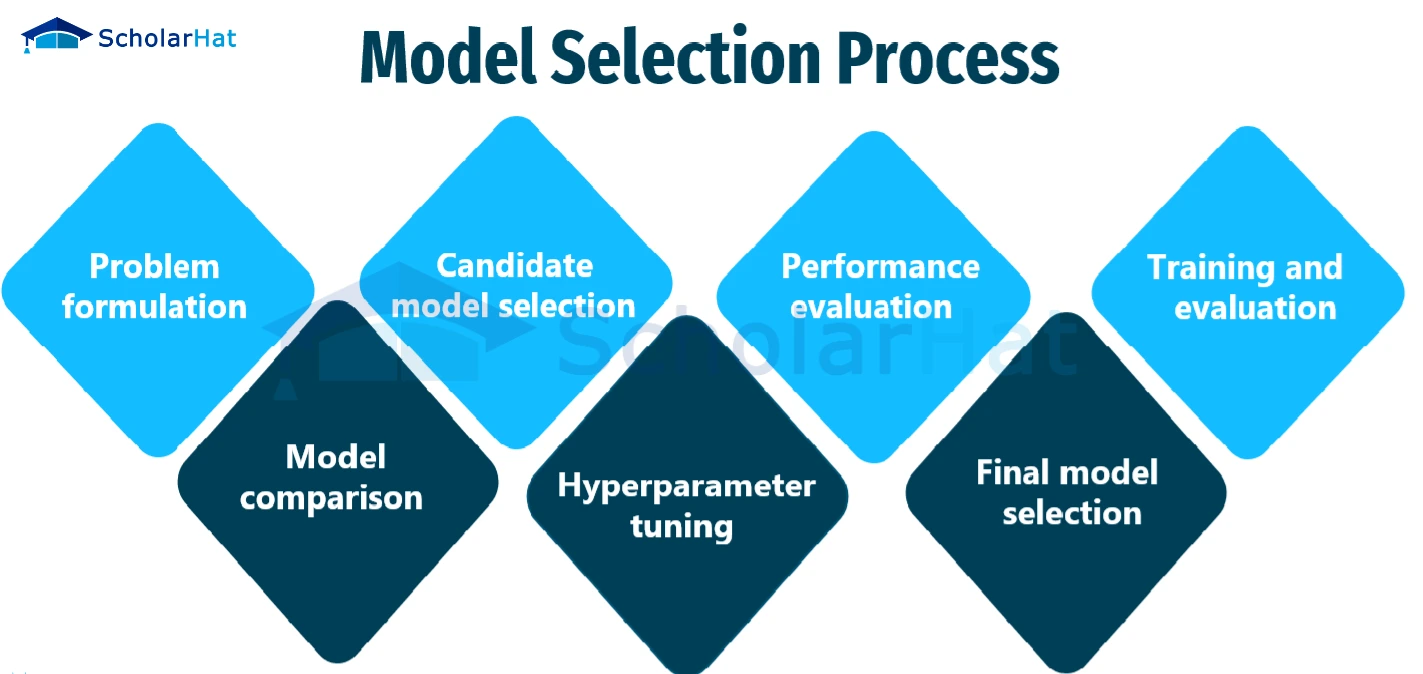
• Problem formulation: Clearly express the issue at hand, including the kind of predictions or task that you'd like the model to carry out (for example, classification, regression, or clustering).
• Candidate model selection: Pick a group of models that are appropriate for the issue at hand. These models can include straightforward methods like decision trees or linear regression as well as more sophisticated ones like deep neural networks, random forests, or support vector machines.
• Performance evaluation: Establish measures for measuring how well each model performs. Common measurements include area under the receiver's operating characteristic curve (AUC-ROC), recall, F1-score, mean squared error, and accuracy, precision, and recall. The type of problem and the particular requirements will determine which metrics are used.
• Training and evaluation: Each candidate model should be trained using a subset of the available data (the training set), and its performance should be assessed using a different subset (the validation set or via cross-validation). The established evaluation measures are used to gauge the model's effectiveness.
• Model comparison: Evaluate the performance of various models and determine which one performs best on the validation set. Take into account elements like data handling capabilities, interpretability, computational difficulty, and accuracy.
• Hyperparameter tuning: Before training, many models require that certain hyperparameters, such as the learning rate, regularisation strength, or the number of layers that are hidden in a neural network, be configured. Use methods like grid search, random search, and Bayesian optimization to identify these hyperparameters' ideal values.
• Final model selection: After the models have been analyzed and fine-tuned, pick the model that performs the best. Then, this model can be used to make predictions based on fresh, unforeseen data.

Model Selection in machine learning:

Model selection in machine learning is the process of selecting the best algorithm and model architecture for a specific job or dataset. It entails assessing and contrasting various models to identify the one that best fits the data & produces the best results. Model complexity, data handling capabilities, and generalizability to new examples are all taken into account while choosing a model. Models are evaluated and contrasted using methods like cross-validation, and grid search, as well as indicators like accuracy and mean squared error. Finding a model that balances complexity and performance to produce reliable predictions and strong generalization abilities is the aim of model selection.

There are numerous important considerations to bear in mind while selecting a model for machine learning. These factors assist in ensuring that the chosen model is effective in solving the issue at its core and has an opportunity for outstanding performance. Here are some crucial things to remember:

• The complexity of the issue: Determine how complex the issue you're trying to resolve is. Simple models might effectively solve some issues, but more complicated models can be necessary to fully represent complex relationships in the data. Take into account the size of the dataset, the complexity of the input features, and any potential for non-linear connections.
• Data Availability & Quality: Consider the accessibility and caliber of the data you already have. Using complicated models with a lot of parameters on a limited dataset may result in overfitting. Such situations may call for simpler models with fewer parameters. Take into account missing data, outliers, and noise as well as how various models respond to these difficulties.
• Interpretability: Consider whether the model's interpretability is crucial in your particular setting. Some models, like decision trees or linear regression, offer interpretability by giving precise insights into the correlations between the input data and the desired outcome. Complex models, such as neural networks, may perform better but offer less interpretability.
• Model Assumptions: Recognise the presumptions that various models make. For instance, although decision trees assume piecewise constant relationships, linear regression assumes a linear relationship between the input characteristics and the target variable. Make sure the model you choose is consistent with the fundamental presumptions underpinning the data and the issue.
• Scalability and Efficiency: If you're working with massive datasets or real-time applications, take the model's scalability and computing efficiency into consideration. Deep neural networks and support vector machines are two examples of models that could need a lot of time and computing power to train.
• Regularisation and Generalisation: Assess the model's capacity to apply to fresh, untested data. By including penalty terms to the objective function of the model, regularisation approaches like L1 or L2 regularisation can help prevent overfitting. When the training data is sparse, regularised models may perform better in terms of generalization.
• Domain Expertise: Consider your expertise and domain knowledge. On the basis of previous knowledge of the data or particular features of the domain, consider if particular models are appropriate for the task. Models that are more likely to capture important patterns can be found by using domain expertise to direct the selection process.
• Resource Constraints: Take into account any resource limitations you may have, such as constrained memory space, processing speed, or time. Make that the chosen model can be successfully implemented using the resources at hand. Some models require significant resources during training or inference.
• Ensemble Methods: Examine the potential advantages of ensemble methods, which integrate the results of various models in order to perform more effectively. By utilizing the diversity of several models' predictions, ensemble approaches, such as bagging, boosting, and stacking, frequently outperform individual models.
• Evaluation and Experimentation: experimentation and assessment of several models should be done thoroughly. Utilize the right evaluation criteria and statistical tests to compare their performance. To evaluate the models' performance on unknown data and reduce the danger of overfitting, use hold-out or cross-validation.

Model Selection Techniques

Model selection in machine learning can be done using a variety of methods and tactics. These methods assist in comparing and assessing many models to determine which is best suited to solve a certain issue. Here are some methods for selecting models that are frequently used:

• Train-Test Split: With this strategy, the available data is divided into two sets: a training set & a separate test set. The models are evaluated using a predetermined evaluation metric on the test set after being trained on the training set. This method offers a quick and easy way to evaluate a model's performance using hypothetical data.
• Cross-Validation: A resampling approach called cross-validation divides the data into various groups or folds. Several folds are used as the test set & the rest folds as the training set, and the models undergo training and evaluation on each fold separately. Lowering the variance in the evaluation makes it easier to generate an accurate assessment of the model's performance. Cross-validation techniques that are frequently used include leave-one-out, stratified, and k-fold cross-validation.
• Grid Search: Hyperparameter tuning is done using the grid search technique. In order to do this, a grid containing hyperparameter values must be defined, and all potential hyperparameter combinations must be thoroughly searched. For each combination, the models are trained, assessed, and their performances are contrasted. Finding the ideal hyperparameter settings to optimize the model's performance is made easier by grid search.
• Random Search: A set distribution for hyperparameter values is sampled at random as part of the random search hyperparameter tuning technique. In contrast to grid search, which considers every potential combination, random search only investigates a portion of the hyperparameter field. When a thorough search is not possible due to the size of the search space, this strategy can be helpful.
• Bayesian optimization: A more sophisticated method of hyperparameter tweaking, Bayesian optimization. It models the relationship between the performance of the model and the hyperparameters using a probabilistic model. It intelligently chooses which set of hyperparameters to investigate next by updating the probabilistic model and iteratively assessing the model's performance. When the search space is big and expensive to examine, Bayesian optimization is especially effective.
• Model averaging: This technique combines forecasts from various models to get a single prediction. For regression issues, this can be accomplished by averaging the predictions, while for classification problems, voting or weighted voting systems can be used. Model averaging can increase overall prediction accuracy by lowering the bias and variation of individual models.
• Information Criteria: Information criteria offer a numerical assessment of the trade-off between model complexity and goodness of fit. Examples include the Akaike Information Criterion (AIC) and the Bayesian Information Criterion (BIC). These criteria discourage the use of too complicated models and encourage the adoption of simpler models that adequately explain the data.
• Domain Expertise & Prior Knowledge: Prior understanding of the problem and the data, as well as domain expertise, can have a significant impact on model choice. The models that are more suitable given the specifics of the problem and the details of the data may be known by subject matter experts.
• Model Performance Comparison: Using the right assessment measures, it is vital to evaluate the performance of various models. Depending on the issue at hand, these measurements could include F1-score, mean squared error, accuracy, precision, recall, or the area beneath the receiver's operating characteristic curve (AUC-ROC). The best-performing model can be found by comparing many models.

Summary

The important machine learning stage of model selection entails selecting the best model and algorithm for a certain task. To make precise predictions on unknown data, it is crucial to find a balance between model complexity & generalization. Model selection involves selecting potential candidates, assessing each model's performance, and selecting the model with the best results.

Assessing the problem's complexity, data quality and availability, interpretability, model assumptions, scalability, efficiency, regularisation, domain knowledge, resource restrictions, and the possible advantages of ensemble approaches are all factors that should be taken into account when choosing a model. These factors aid in ensuring that the chosen model complies with the limits and needs of the issue.

There are many methods for choosing a model, such as train-test split, cross-validation, grid searches, random search, Bayesian optimization, model averaging, information criteria, expertise in the domain, and model performance comparison. These methods make it possible to thoroughly assess, tune hyperparameters, and compare various models to get the best fit.