Bucket Sort in Data Structures

Bucket Sort: An Overview

In this DSA tutorial, we will understand a sorting algorithm called Bucket Sort that distributes the array elements into various groups or buckets and then performs sorting. We will look at its technique, working, implementation, etc. To further enhance your understanding and application of bubble sort, consider enrolling in the Dsa Course, to gain comprehensive insights into effective data structure utilization for improved problem-solving and time management.

What is Bucket Sort in Data Structures?

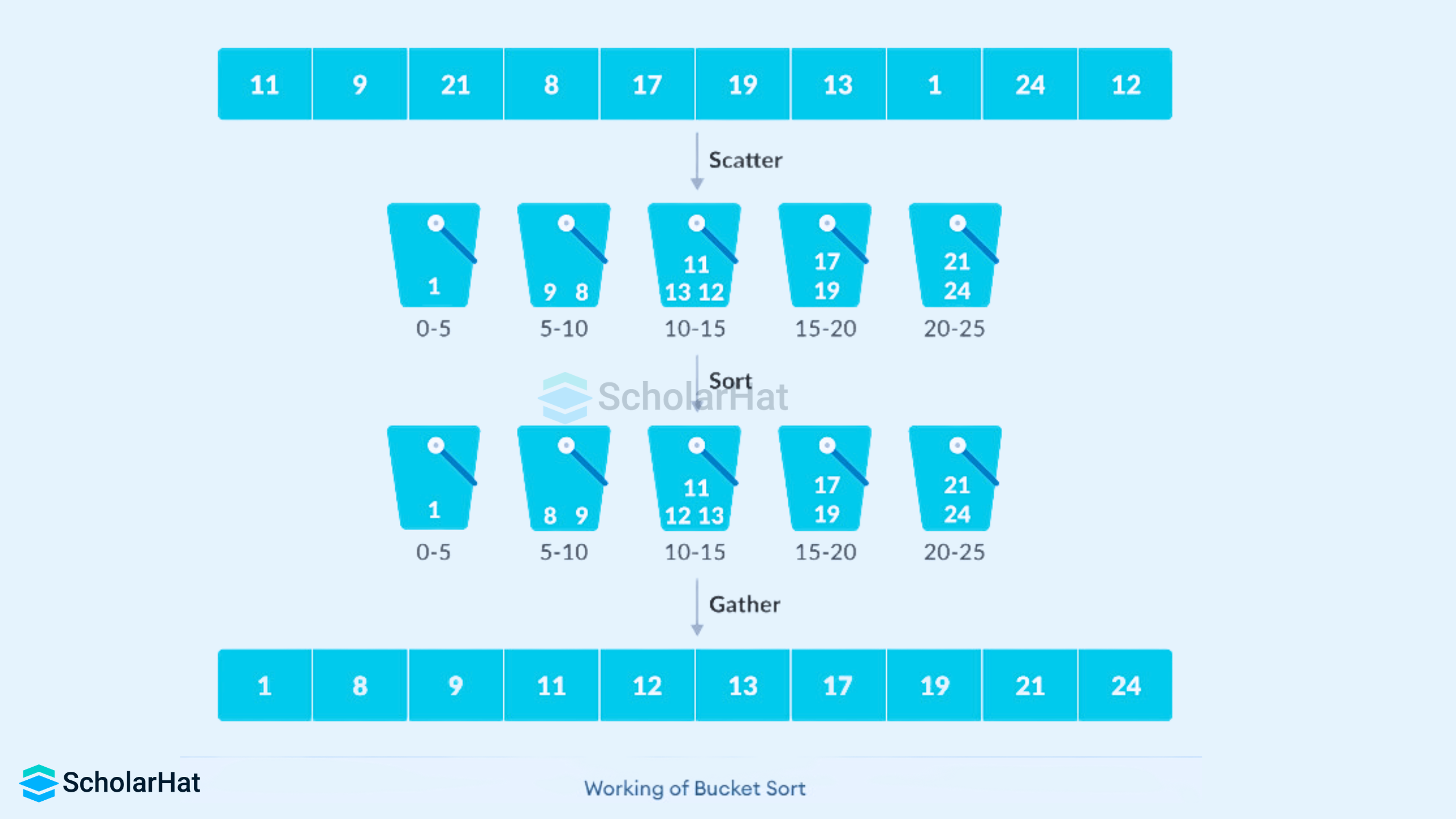
Bucket sort works according to the scatter-and-gather approach. It first of all divides the unsorted array into various groups or buckets. These buckets are used to store data having similar values, and then it applies any of the sorting techniques or recursively applies the same bucket algorithm on each bucket to get the sorted list. Afterward, the sorted buckets are combined to form a final sorted array.

It works on uniformly distributed data i.e. the difference between every adjacent element is almost the same. For example, [10, 21, 29, 41, 52] Here, the difference between each adjacent term is almost equal to 10. Hence, this array has uniformly distributed data and can be sorted using the bucket sort algorithm.

Scatter-Gather Approach: The Underlying Principle

The scatter-gather approach tries to simplify complex problems by first scattering the complete data into groups or buckets, solving these sub-problems individually, and finally gathering them all together to get the final result.

Read More - Best Data Structure Interview Questions and Answers

Bucket Sort Algorithm

bucketSort()
  create N buckets each of which can hold a range of values
  for all the buckets
    initialize each bucket with 0 values
  for all the buckets
    put elements into buckets matching the range
  for all the buckets 
    sort elements in each bucket
  gather elements from each bucket
end bucketSort

Working of Bucket Sort Algorithm

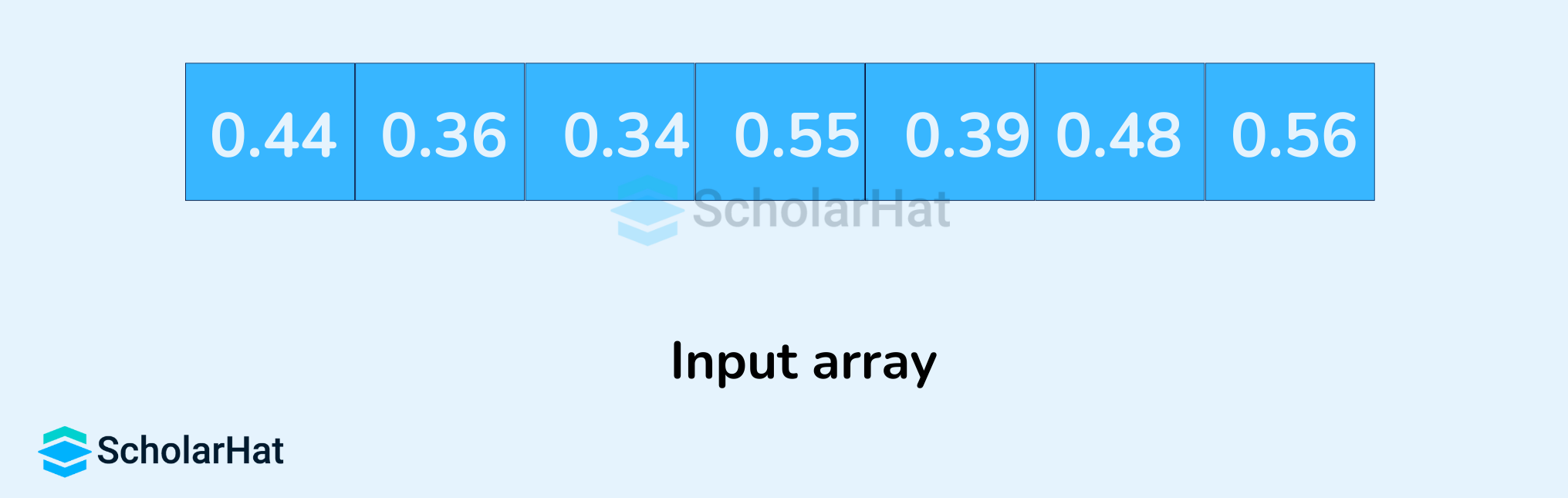
1. Let's suppose, the input array is:

   

   Create an array of size 10. Each slot of this array is used as a bucket for storing elements.

   

2. Insert elements into the buckets from the array. The elements are inserted according to the range of the bucket.

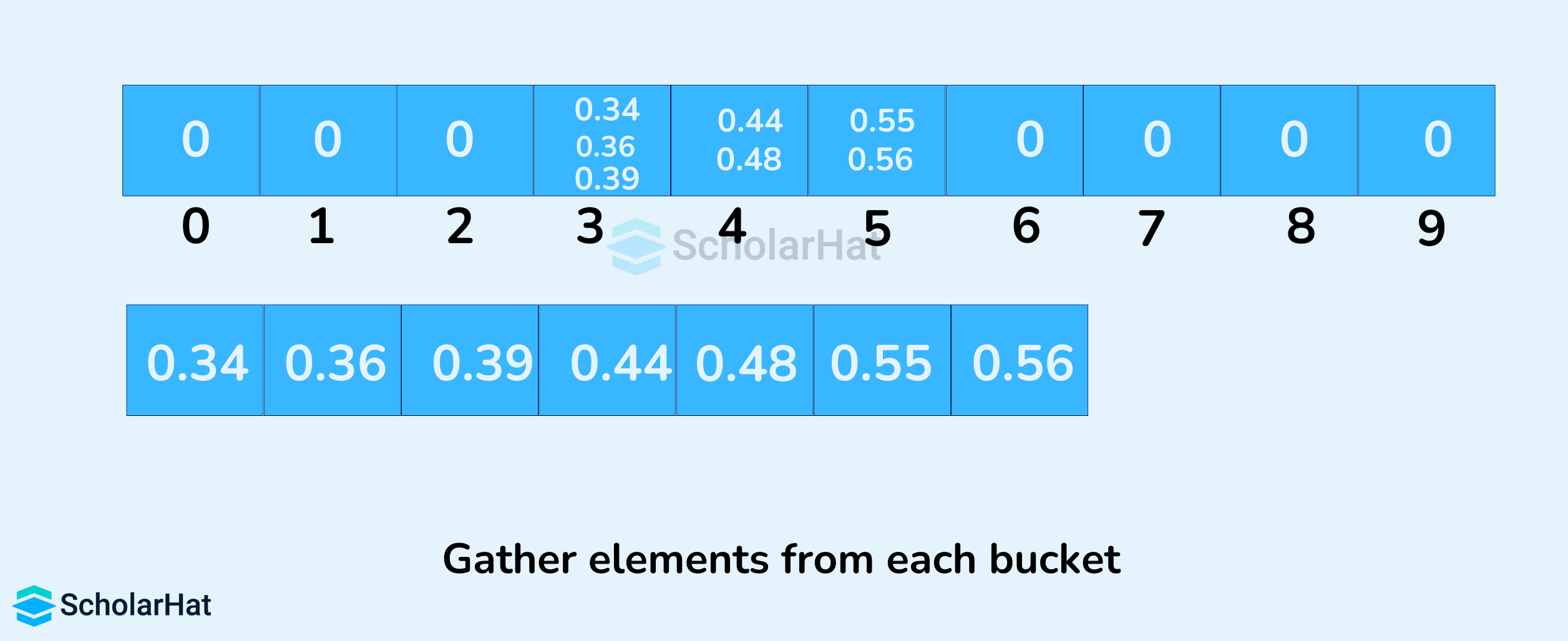
   In our example, we have buckets of ranges from 0 to 1, 1 to 2, 2 to 3,...... (n-1) to n. Suppose, an input element is .34 is taken. It is multiplied by size = 10 (ie. .34*10=3.4) Then, it is converted into an integer (ie. 3.4≈3). Finally, .34 is inserted into bucket 3.

   

   If we take integer numbers as input, we have to divide it by the interval (10 here) to get the floor value.

   Similarly, other elements are inserted into their respective buckets.

   

3. The elements of each bucket are sorted using any of the stable sorting algorithms. Here, we have used quicksort (inbuilt function).

   

4. The elements from each bucket are gathered. It is done by iterating through the bucket and inserting an individual element into the original array in each cycle. The element from the bucket is erased once it is copied into the original array.

Implementation of Bucket Sort in Different Languages in Data Structures

def bucketSort(array):
    bucket = []

    # Create empty buckets
    for i in range(len(array)):
        bucket.append([])

    # Insert elements into their respective buckets
    for j in array:
        index_b = int(10 * j)
        bucket[index_b].append(j)

    # Sort the elements of each bucket
    for i in range(len(array)):
        bucket[i] = sorted(bucket[i])

    # Get the sorted elements
    k = 0
    for i in range(len(array)):
        for j in range(len(bucket[i])):
            array[k] = bucket[i][j]
            k += 1
    return array

def print_list(arr):
    for i in range(len(arr)):
        print(arr[i], end=" ")
    print()

array = [.44, .36, .34, .55, .39, .48, .56]

# Print the original array
print('Original Array:', end=" ")
print_list(array)

(bucketSort(array))

# Print the sorted array in aescending order
print('Sorted Array in Aescending Order:', end=" ")
print_list(array)
    

import java.util.ArrayList;
import java.util.Collections;
import java.util.List;

public class BucketSort {
    static double[] bucketSort(double[] array) {
        int n = array.length;
        List[] bucket = new ArrayList[n];

        // Create empty buckets
        for (int i = 0; i < n; i++) {
            bucket[i] = new ArrayList<>();
        }

        // Insert elements into their respective buckets
        for (double j : array) {
            int indexB = (int) (10 * j);
            bucket[indexB].add(j);
        }

        // Sort the elements of each bucket
        for (int i = 0; i < n; i++) {
            Collections.sort(bucket[i]);
        }

        // Get the sorted elements
        int k = 0;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < bucket[i].size(); j++) {
                array[k] = bucket[i].get(j);
                k++;
            }
        }

        return array;
    }

    static void printArray(double[] arr) {
        for (double i : arr) {
            System.out.print(i + " ");
        }
        System.out.println();
    }

    public static void main(String[] args) {
        double[] array = {0.44, 0.36, 0.34, 0.55, 0.39, 0.48, 0.56};

        // Print the original array
        System.out.print("Original Array: ");
        printArray(array);

        // Sort the array
        bucketSort(array);

        // Print the sorted array in aescending order
        System.out.print("Sorted Array in Aescending Order: ");
        printArray(array);
    }
}
    

#include <iomanip>
#include <iostream>
#include <cstdlib>
#include <vector>
using namespace std;

#define NARRAY 7   // Array size
#define NBUCKET 6  // Number of buckets
#define INTERVAL 0.1  // Each bucket capacity

struct Node {
  double data;
  struct Node *next;
};

void BucketSort(double arr[]);
struct Node *InsertionSort(struct Node *list);
void print(double arr[]);
void printBuckets(struct Node *list);
int getBucketIndex(double value);

// Sorting function
void BucketSort(double arr[]) {
  int i, j;
  struct Node **buckets;

  // Create buckets and allocate memory size
  buckets = (struct Node **)malloc(sizeof(struct Node *) * NBUCKET);

  // Initialize empty buckets
  for (i = 0; i < NBUCKET; ++i) {
    buckets[i] = NULL;
  }

  // Fill the buckets with respective elements
  for (i = 0; i < NARRAY; ++i) {
    struct Node *current;
    int pos = getBucketIndex(arr[i]);
    current = (struct Node *)malloc(sizeof(struct Node));
    current->data = arr[i];
    current->next = buckets[pos];
    buckets[pos] = current;
  }

  // Print the buckets along with their elements
  for (i = 0; i < NBUCKET; i++) {
    cout << "Bucket[" << i << "] : ";
    printBuckets(buckets[i]);
    cout << endl;
  }

  // Sort the elements of each bucket
  for (i = 0; i < NBUCKET; ++i) {
    buckets[i] = InsertionSort(buckets[i]);
  }

  cout << "-------------" << endl;
  cout << "Buckets after sorted" << endl;
  for (i = 0; i < NBUCKET; i++) {
    cout << "Bucket[" << i << "] : ";
    printBuckets(buckets[i]);
    cout << endl;
  }

  // Put sorted elements back into arr
  for (j = 0, i = 0; i < NBUCKET; ++i) {
    struct Node *node;
    node = buckets[i];
    while (node) {
      arr[j++] = node->data;
      node = node->next;
    }
  }

  // Free allocated memory
  for (i = 0; i < NBUCKET; ++i) {
    struct Node *node;
    node = buckets[i];
    while (node) {
      struct Node *tmp;
      tmp = node;
      node = node->next;
      free(tmp);
    }
  }
  free(buckets);
  return;
}

// Function to sort the elements of each bucket
struct Node *InsertionSort(struct Node *list) {
  struct Node *k, *nodeList;
  if (list == 0 || list->next == 0) {
    return list;
  }

  nodeList = list;
  k = list->next;
  nodeList->next = 0;
  while (k != 0) {
    struct Node *ptr;
    if (nodeList->data > k->data) {
      struct Node *tmp;
      tmp = k;
      k = k->next;
      tmp->next = nodeList;
      nodeList = tmp;
      continue;
    }

    for (ptr = nodeList; ptr->next != 0; ptr = ptr->next) {
      if (ptr->next->data > k->data)
        break;
    }

    if (ptr->next != 0) {
      struct Node *tmp;
      tmp = k;
      k = k->next;
      tmp->next = ptr->next;
      ptr->next = tmp;
      continue;
    } else {
      ptr->next = k;
      k = k->next;
      ptr->next->next = 0;
      continue;
    }
  }
  return nodeList;
}

int getBucketIndex(double value) {
  return value / INTERVAL;
}

// Print buckets
void print(double arr[]) {
  int i;
  for (i = 0; i < NARRAY; ++i) {
    cout << setw(4) << arr[i] << ",";
  }
  cout << endl;
}

void printBuckets(struct Node *list) {
  struct Node *cur = list;
  while (cur) {
    cout << setw(4) << ", " << cur->data;
    cur = cur->next;
  }
}

// Driver code
int main(void) {
  double array[NARRAY] = {0.44, 0.36, 0.34, 0.55, 0.39, 0.48, 0.56};

  cout << "Initial array: " << endl;
  print(array);
  cout << "-------------" << endl;

  BucketSort(array);
  cout << "-------------" << endl;
  cout << "Sorted array: " << endl;
  print(array);

  return 0;
}
    

Output

Initial array: 
0.44,0.36,0.34,0.55,0.39,0.48,0.56,
-------------
Bucket[0] : 
Bucket[1] : 
Bucket[2] : 
Bucket[3] :   , 0.39  , 0.34  , 0.36
Bucket[4] :   , 0.48  , 0.44
Bucket[5] :   , 0.56  , 0.55
-------------
Buckets after sorted
Bucket[0] : 
Bucket[1] : 
Bucket[2] : 
Bucket[3] :   , 0.34  , 0.36  , 0.39
Bucket[4] :   , 0.44  , 0.48
Bucket[5] :   , 0.55  , 0.56
-------------
Sorted array: 
0.34,0.36,0.39,0.44,0.48,0.55,0.56,

Complexity Analysis of Bucket Sort Algorithm

1. Time Complexity

   Case	Time Complexity
   Best	O(n+k)
   Average	O(n)
   Worst	O(n^2)

2. Space Complexity: The Space Complexity for bucket sort is O(n+k), where n = number of elements in the array, and k = number of buckets formed. Space taken by each bucket is O(k)and inside each bucket, we have n elements scattered.

Applications of Bucket Sort Algorithm

1. Sorting floating-point numbers:Bucket sort is particularly suitable for sorting floating-point numbers within a specific range. For example, if you have a large set of numbers between 0 and 1, you can divide this range into multiple buckets and distribute the numbers accordingly.
2. Sorting integers within a range: Similar to sorting floating-point numbers, bucket sort can efficiently sort integers within a specific range. For example, if you have a set of integers between 1 and 1,000, you can divide this range into multiple buckets and distribute the integers accordingly.
3. Sorting data with known distributions: If you have prior knowledge about the distribution of the input data, such as a uniform or Gaussian distribution, bucket sort can be used
4. Radix sort optimization: Bucket sort is often used as a sub-routine in the radix sort algorithm. It uses bucket sort to sort the numbers based on each digit, achieving efficient overall performance.

Advantages of Bucket Sort Algorithm

1. Efficiency for uniformly distributed data: Bucket sort performs efficiently when the input data is uniformly distributed across a range. It can distribute the elements evenly into buckets, leading to a more balanced workload during the sorting process.
2. Simplicity: Bucket sort is relatively easy to understand and implement compared to other sorting algorithms like quick sort or merge sort.
3. The linear time complexity for specific cases: In the best-case scenario, where the elements are uniformly distributed across the buckets and the number of elements in each bucket is small, bucket sort can achieve linear time complexity.

Disadvantages of Bucket Sort Algorithm

1. Limited Applicability: Bucket sort is most effective when the input data is uniformly distributed across the range of possible values. Uneven distribution can lead to imbalanced buckets, resulting in poor sorting performance.
2. Memory Requirements: Bucket sort requires additional memory space to create the buckets and hold the elements within each bucket. The number of buckets needed depends on the range of input values. If the range is large, a significant amount of memory may be required, which can be a constraint for systems with limited memory resources.
3. Limited Sorting of Non-Integer Data: Bucket sort is primarily designed for sorting integers or floating-point numbers. It may not be directly applicable to sorting other types of data, such as strings or complex objects. Adapting bucket sorting for non-numeric data would require additional preprocessing steps or customizations.

Summary

So, here we saw every aspect of the bucket sort algorithm in data structures. It must have been a little difficult to understand the implementation of it in programming. But, not to worry. After a time, you won't find it. To apply your knowledge of the bucket sort algorithm, enroll in our Free Dsa Course With Certificate.

Similar Sorting Algorithms

• Insertion Sort
• Merge Sort
• Quick Sort
• Bubble Sort